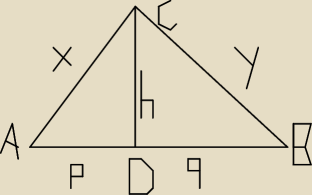
planimetria sys: Z wierzchołka C kąta prostego trójkąta prostokątnego ABC poprowadzono wysokość h na przeciwprostokątną AB. Spodek wysokości D podzielił przeciwprostokątną na odcinki p i q. Wykaż, że długość wysokości h jest średnią geometryczną długości odcinków p i q, czyli że h=√pq proszę o wyjaśnienie a nie rozwiązanie, może mi ktoś wytłumaczyć to podobieństwo trójkątów bo z tego trzeba tu skorzystać

sys:

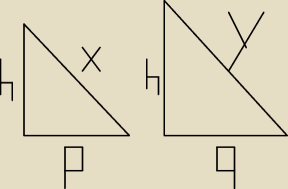
	h		q
bok, kąt, bok? czyli		=
	p		p

sys:

h		q
	=
p		h

sys: czy można tu zastosować inne cechy podobieństwa ?

mlodyfizyk: Też nie rozumiem tego zadania,a jutro mam sprawdzian z planimetrii.

sys: nikt?

mlodyfizyk: Ja robiłem tak samo jak ty bok,kąt,bok,ale nie mam pojęcia czy można inne cechy zastosować.

sys: HELP!

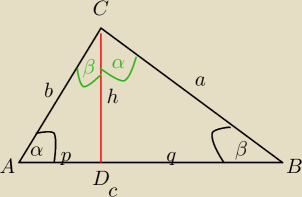
Mila: ΔADC∼ΔCDB cecha kkk ⇔

p		h
	=		⇔h2=p*q⇔h=√p*q −średnia geometryczna
h		q

Możesz ułożyć inne proporcje:

p		h
	=
b		a

q		h
	=
a		b

ΔADC∼ΔABC ceha kkk

p		b
	=		⇔b2=p*c
b		c

ΔCDB∼ΔCDB cecha kkk

q		a
	=		⇔a2=q*c
a		c

sys: dziękuję Mila

sys: a ten wzór co jest w tablicach matematycznych h² = IADI * IDBI można jakoś wykorzystać

Mila: To przecież jest właśnie średnia geometryczna p i q ( wg Twoich oznaczeń). Możesz wykorzystywać w zadaniach. Konkretnie do czego chcesz wykorzystać?