Okrag w ukladzie kartezjanskim
Piotrek: | | 1 | |
Znalezc rownanie okregu stycznego do osi Ox oraz do obu galezi krzywej o rownaniu y= |
| |
| | x2 | |
Wskazowka Skorzystac z algebraicznego warunku stycznosci
17 mar 15:22
Janek191:
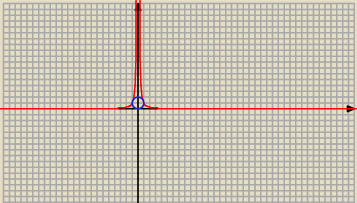
S = ( 0; r ) ; r > 0
| | 1 | | 1 | |
y = |
| ⇒ 1 = y*x2 ⇒ x2 = |
| |
| | x2 | | y | |
Równanie okręgu
( x − 0)
2 + ( y − r)
2 = r
2
więc
x
2 + y
2 − 2r y + r
2 = r
2
1 + y
3 −2 r y
2 = 0
y
3 − 2r y
2 + 1 = 0
Dla r = 1 mamy y
3 − 2 y
2 + 1 = 0 ⇒ y = 1
Wtedy
| | 1 | |
x2 = |
| = 1 ⇒ x = − 1 lub x = 1 |
| | 1 | |
P
1 = ( 1; 1) P
2 = ( − 1; 1) − punkty styczności
Odp. Równanie okręgu : x
2 + ( y − 1)
2 = 1
================================
17 mar 16:12
Hajtowy: Janek191 mam prośbę

Możesz nie rozwiązywać każdemu w 100% zadań? Pasuje, żeby się coś
ta młodzież nauczyła bo kto Ci będzie na emeryturę zarabiał?

17 mar 16:14
walt: "Dla r=1", skąd wiemy, że r=1?
17 mar 16:24
J: Tylko taki okrąg wchodzi w grę ... Punkt styczności musi być równodległy od osi OX i OY i
należeć do hiperboli, a tym punktem jest (1,1) lub (−1,1)
17 mar 16:32
walt: dzięki
17 mar 16:33
...:
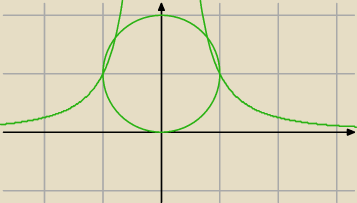
... niestety to nie całkiem prawda lub "g" prawda −

17 mar 16:59
Janek191:
To zawaliłem

Przepraszam. Jednak rysunek, to połowa sukcesu.
17 mar 17:06
...:
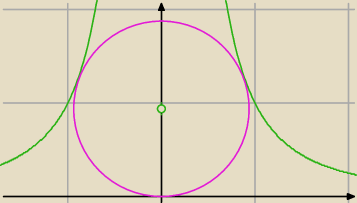
17 mar 17:23
 S = ( 0; r ) ; r > 0
S = ( 0; r ) ; r > 0
 Możesz nie rozwiązywać każdemu w 100% zadań? Pasuje, żeby się coś
ta młodzież nauczyła bo kto Ci będzie na emeryturę zarabiał?
Możesz nie rozwiązywać każdemu w 100% zadań? Pasuje, żeby się coś
ta młodzież nauczyła bo kto Ci będzie na emeryturę zarabiał? 
 ... niestety to nie całkiem prawda lub "g" prawda −
... niestety to nie całkiem prawda lub "g" prawda −
 Przepraszam. Jednak rysunek, to połowa sukcesu.
Przepraszam. Jednak rysunek, to połowa sukcesu.
