analityczna
Radek:
Punkty A = (− 2,0) i B = (8,0) są wierzchołkami trójkąta prostokątnego ABC o
przeciwprostokątnej AB i polu równym 15. Oblicz współrzędne punktu C
proszę o jakieś naprowadzenie
16 mar 23:42
...:
... pole .... to podstawa razy wysokość
Twoja wysokość to odległość punktu C od prostej przechodzącej przez A i B
16 mar 23:45
Radek:
mam AB=10
16 mar 23:47
...:
... a można C=(xc, yc)
policzyć |AC| i |BC| i z nich pole
Pitagorasek też może pomóc
16 mar 23:48
Radek: ?
16 mar 23:54
16 mar 23:56
Marcin: C=(x,y)
Policz odległość C od A
Policz odległość C od B
Następnie wykorzystaj twierdzenie pitagorasa

(przeciwprostokątna =10)
16 mar 23:57
Mila:
Radek?
17 mar 00:03
Mila: No to dobranoc

17 mar 00:04
Radek:
Może Pani jeszcze chwilkę zostać

17 mar 00:05
Radek: h=3
17 mar 00:06
Mila:
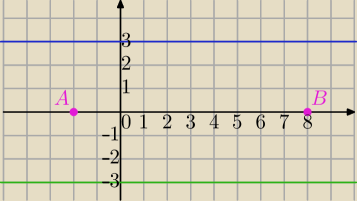
Podpowiedź:
C leży na prostej y=3 ⇔ma wsp. C=(c,3)
albo C
C leży na prostej y=−3 ⇔ma wsp. C=(c,−3)
1) Tw. Pitagorasa
albo
2) Wykorzystaj tw. kąt wpisany w okrąg oparty na średnicy jest prosty.
17 mar 14:40
Radek:
Czemu Pani korzysta akurat z okręgu ?
17 mar 17:44
Mila:
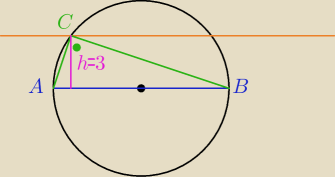
∡C=90
o jako wpisany oparty na średnicy.
17 mar 17:47
Radek:
No tak ale czemu akurat z tego warunku Pani korzysta, ja nie mam w zadaniu okręgu
17 mar 17:49
Mila:
To go narysuj. Przecież w zadaniach geometrycznych rysujemy linie pomocnicze, okrąg też może
być linią pomocniczą.
17 mar 17:52
Radek:
No tak ale czy nie można np z twierdzenia pitagorasa ?
17 mar 18:16
Marcin: Można. Przecież MIla Ci to napisała

17 mar 18:22
Mila:
Radek, pierwszy sposób podałam z tw. Pitagorasa, potem napisałam albo.
Ciągle boisz się innych sposobów.
Z Pitagorasa będziesz miał sporo liczenia.
Policz z tw. Pitagorasa, a potem skorzystaj z mojego sposobu.
Umiesz przecież napisać równanie okręgu o środku (3,0) i r=5. Nie bój się okręgi nie gryzą.
17 mar 18:30
Mila:
3) sposób najprostszy:
Wektory
CA→⊥CB→
17 mar 18:32
Radek:
Wychodzą dwa rozwiązania ?
17 mar 18:46
Marcin: Tak, tak

17 mar 18:48
Mila:
4 rozwiązania.
Napisz jakie?
17 mar 18:56
Marcin: Fakt. Wybacz to wprowadzenie w błąd

17 mar 19:02
Radek:
(−1.3) (8,3)
17 mar 19:10
Marcin: Ja mam (−1;3) i (7,3)
Teraz jeszcze rozwiązania z y=−3

17 mar 19:17
Mila:
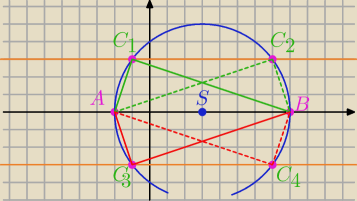
h
Δ=3
S=(3,0)
(x−3)
2+y
2=25
y=3 lub y=−3
(x−3)
2+9=25⇔(x−3)
2=16⇔
x−3=4 lub x−3=−4
x=7 lub x=−1
C
1=(−1,3)
C
2=(7,3)
C
3=(−1,−3)
C
4=(7,−3)
17 mar 19:43
Radek: Dziękuję ale mam jeszcze pytania:
1. Czy sposób z kręgiem zawsze działa dla trójkąta prostokątnego ?
2. Co w wypadku czworokąta ?
17 mar 19:49
Mila:
Radek, tu wyraźnie podano, że masz daną przeciwprostokątną i szukasz przyprostokątnych.
W tym zadaniu często uczniowie popełniają błąd.
Nie wiem jakie zadanie z czworokątem masz na myśli.
Jak to w końcu zrobiłeś?
17 mar 20:11
Radek:
Tym sposobem który podała Pani. Ale chodzi mi o zadania typu, w treści jest podane, że jest to
trójkat prostokątny i mam dwa punkt i trzeba znaleźć 3 wierzchołek
2.Współrzędne przeciwległych wierzchołków prostokąta ABCD są równe A = (5,− 3), C = (− 7,1) .
Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek B leży na
prostej y = 5
17 mar 20:15
Mila:
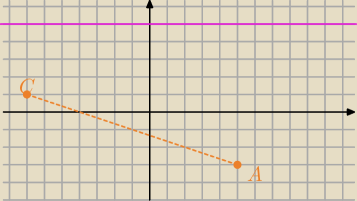
Też tak można.
S − środek AC
Spróbuj tutaj z tw. Pitagorasa
AC
2=AB
2+CB
2
B(x, 5)
Zapisz tu obliczenia, abym widziała, jak to rozwiązujesz.
Już policzyłam.
17 mar 20:33
Radek:
robię tak
współczynnik AC
prosta prostopadła , do prostej AC i przez punkt A
y=3x−18
prosta prostopadła do AC i przez punkt C
y=3x+22
przecięcie się prostej y=3x−18 i y=5
prosta równoległa do prostej AC i mam wszystkie punkty
Wychodzi jedna para rozwiązań
17 mar 20:43
Mila:
To niestety źle robisz . Popełniasz ten błąd o którym pisałam. Przecież nie jest Ci potrzebna
prosopadła do przekątnej!
Spróbuj tutaj z tw. Pitagorasa tak: (narysuj sobie to na kartce, odręcznie zaznacz punkt B,
abyś miał kąt prosty ABC)
|AC|2=|AB|2+|CB|2
B(x, 5)
17 mar 21:09
Mila:
Jakie masz punkty ?
17 mar 21:13
Radek:
B=(1,5)
D=(1,6)
17 mar 21:16
Mila:
Zaznacz swoje punkty w układzie i sprawdź , czy AC jest przekątną.
17 mar 21:24
Radek:
Właśnie widzę, że mam błąd. Ja nigdy nie wiem kiedy są dwa rozwiązania w takich konstrukcjach
albo więcej nawet czasami ?
17 mar 21:25
Marcin: Ale Radku B masz chyba dobrze. Tylko że jeszcze powinieneś mieć jeden punkt (−3;5) (dla B)
I z tego jeszcze dwa razy D.
O ile się nie mylę oczywiście..
17 mar 21:29
Mila:
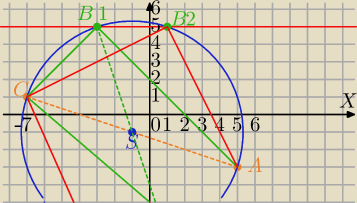
I sposób.
|AC|=
√42+122=
√16+144=
√160=4
√10
| | −7+5 | | 1−3 | |
S=( |
| , |
| )=(−1,−1) |
| | 2 | | 2 | |
"Kreślę" okrąg
(x+1)
2+(y+1)
2=(2
√19)
2 otrzymuję dwa punkty przecięcia z prostą y=5
podstawiam
(x+1)
2+6
2=4*10
(x+1)
2=4
x+1=2 lub x+1 =−2
x=1 lub x=−3
B
1=(−3,5) lub B
2=(1,5)
szukamy D
1 ,D
2 jako punktów symetrycznych względem S
D
1=(1,−7)
Oblicz D
2
17 mar 21:44
Radek:
D2 = (− 3,− 7)
Tylko teraz mam prostokąt a Pani kreśli też na okręgu ?
17 mar 21:46
Mila:
II sposób
( to zadanie takim sposobem może lepiej) − tak Ci radziłam, nie posłuchałeś.
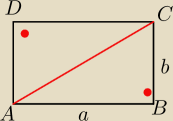
Z tw. Pitagorasa (kąt prosty w wierzchołku B)
|AC|2=|AB|2+|CB|2
B(x, 5)
AC2=160
(x−5)2+(5+3)2+(x+7)2+(5−1)2=160
z tego masz:
x2+2x−3=0
x=−3 lub x=1
B1=(−3,5)
B2=(1,5) teraz wyznaczasz punkty D1 i D2 jako symetryczne względem punktu przecięcia
przekątnych.
17 mar 21:51
Marcin: Bo to kwadrat wyszedł

17 mar 21:51
Radek:
Ale ja nadal nie rozumiem czemu tw pitago skoro mam prostokąt?
17 mar 21:52
Mila:
17 mar 21:55
Radek:
Dobrze postaram się to zrozumieć a teraz mam trudniejsze wgl nie wiem jak zacząć nawet
Punkt A = (3,1),B = (7,3) są kolejnymi wierzchołkami kwadratu ABCD . Wyznacz współrzędne
pozostałych wierzchołków tego kwadratu.
policzyłem długość odcinka AB i teraz będą dwie proste równoległe odalone od prostej AB o
długość odcinka AB ?
17 mar 22:00
Mila:
Teraz rąbiesz prostopadłe do AB w końcach odcinka .
Potem pomyśl. wszystkie boki równe.
17 mar 22:03
Marcin: Liczysz równanie AB
później wyznaczasz równanie prostopadłej, przechodzącej przez jeden z punktów np. (3,1)
później liczysz podstawiasz do wzoru na długość odcinka i masz dwa wyniki

Później to samo w drugim punktem.
Wybacz że się wtrącam, ale też się uczę i czasem staram się pomóc

17 mar 22:07
Radek:
Proste prostopadłe do prostej AB ok a co dalej ?
17 mar 22:19
Eta:
Najprostszy sposób :
wektorami 
( szkoda,że nie chcesz się o nich pouczyć)
17 mar 22:38
Mila:
Właśnie to samo mówię.
Wektory bardzo użyteczne. Pozdrawiam Eta. Wieje u Ciebie?
17 mar 22:42
Eta:
Witam
Mila 
wieje i to bardzo
17 mar 22:45
Radek:
Wiem, że wektory pożyteczne ale ja ich wgl nie umiem, nie chcę sotosować bo się pomylę i
zadania nie zrobię
17 mar 22:46
Mila:
No to co zrobiłeś. Napisz te 3 proste.
17 mar 22:51
Radek:
prosta AB
y=0,5x−0,5
y=−2x+15
y=−2x+7
17 mar 22:58
Marcin: |AB|=√20
Teraz masz punkty
A=(1,3) D=(x,−2x+7) Długość AD to przecież też √20 (podstaw do wzoru)
17 mar 23:01
Radek:
A no tak już sobie poradzę, dziękuję. Jeszcze zostały mi tylko 5 zadań których nie umiem
17 mar 23:05
Marcin: Tego typu?
Podawaj treści. Chętnie sam poćwiczę

17 mar 23:06
Radek:
Inny typ.
17 mar 23:08
Radek:
y=−2x+17 taka powinna być

17 mar 23:09
Marcin: No inny typ też może być

Tak z ciekawości. Dużo czasu dziennie spędzasz na nauce matmy? (dość często Cię tu widzę

)
W tym zadaniu które przed chwilą robiłeś bardzo ładne wyniki wychodzą. Ja ogólnie sobie
najpierw rysuje, a później tylko sprawdzam wyniki

17 mar 23:11
Radek:
Ja uczę się tylko matematyki i angielskiego. Oceny już dawno z innych przedmiotów mam
wystawione. Staram się robić 50 zadań dziennie i kilka arkuszy jak pozwoli czas.
17 mar 23:12
Radek: Rozważamy prostokąty, których dwa wierzchołki leżą na odcinku łączącym punkty wspólne osi Ox i
paraboli o równaniu y = x2 − 6x + 5 , a dwa należą do tej paraboli. Wyznacz współrzędne
wierzchołków tego prostokąta, który ma największy obwód.
17 mar 23:12
Mila:
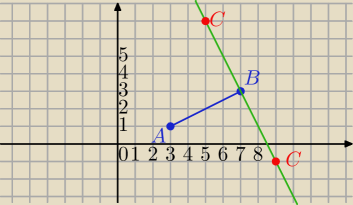
Punkty A = (3,1),B = (7,3) są kolejnymi wierzchołkami kwadratu ABCD'
|AB|=
√42+22=
√20
Prosta AB:
y=ax+b
1=3a+b
3=7a+b
−2=−4a
prosta BC:
y=−2x+b, 3=−2*7+b, b=17
y=−2x+17
C=(x, −2x+17)
|BC|=
√x−7)2+(−2x+17−3)2=
√20⇔
√x−7)2+(−2x+14)2=
√20
|BC|
2=x
2−14x+49+4x
2−56x+196=20
5x
2−70x+225=0/:5
x
2−14x+45=0
licz dalej
17 mar 23:16
Radek:
Też z tego liczyłem i mam takie rozwiązania
C = (5,7),D = (1,5) lub C = (9,− 1),D = (5,− 3) ?
17 mar 23:17
Mila:
No to nie wiem , pomagać , czy nie.
17 mar 23:17
Mila:
Dobrze.
17 mar 23:19
Radek:
Zanim Pani napisała skorzystałem z wskazówki Marcina. A to moje ostatnie zadanie ?
17 mar 23:20
Radek: ?
17 mar 23:29
Marcin: Ciekawe zadanie. Musisz doprowadzić zapewne do funkcji kwadratowej i zbadać jej minimum.
Ale teraz muszę iść spać, bo jutro próbna matura z angielskiego

17 mar 23:32
Radek:
Dziękuję i dobranoc

17 mar 23:33
Marcin: Jeszcze mam tylko jedno pytanie. Skąd Ty bierzesz te zadania i arkusze?

17 mar 23:35
Radek:
Dostaje od Pani i z książki Pazdro również a co ?
17 mar 23:36
Marcin: Też by mi się przydały jakieś nowe zadania

Myślałem że masz to gdzieś na internecie

17 mar 23:37
Mila:
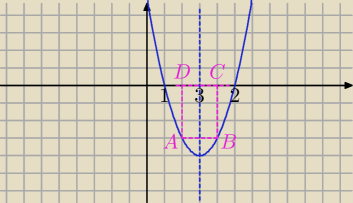
Rysujesz parabolę. ( umiesz?)
y = x
2 − 6x + 5 =(x−3)
2−4
x
w=3
y
w=−4
x=1 lub x=5
Zadanie bardzo pokrętnie podane.
Chodzi o to, że D i C leżą między miejscami zerowymi.?
OBw=2*|AB|+2*|BC|
D=(xd,0) i C=(x
c,0)
x
w jest środkiem DC, osią symetrii paraboli jest prosta x=3
x
c=6−x
d
|DC|=|AB|=x
c−x
d=6−2x
d
Próbuj dalej
A=(x
d, x
d2−6x
d+5)
17 mar 23:43
Radek:
Aż takim ... nie jestem żeby paraboli nie umieć narysować..
Podałem treść prosto z arkusza.
17 mar 23:46
Mila:
Nie do Ciebie, ale do autora mam pretensje.
|AD|=?
17 mar 23:50
Radek:
Nie wiem tutaj nic ?
17 mar 23:57
Mila:
To już jutro wyjaśnimy. Poczytaj co napisałam i zapisz sobie na kartce.
Dobranoc

18 mar 00:02
Radek:
Dziękuję, dobranoc.
18 mar 00:10
 (przeciwprostokątna =10)
(przeciwprostokątna =10)


 Podpowiedź:
C leży na prostej y=3 ⇔ma wsp. C=(c,3)
albo C
C leży na prostej y=−3 ⇔ma wsp. C=(c,−3)
1) Tw. Pitagorasa
albo
2) Wykorzystaj tw. kąt wpisany w okrąg oparty na średnicy jest prosty.
Podpowiedź:
C leży na prostej y=3 ⇔ma wsp. C=(c,3)
albo C
C leży na prostej y=−3 ⇔ma wsp. C=(c,−3)
1) Tw. Pitagorasa
albo
2) Wykorzystaj tw. kąt wpisany w okrąg oparty na średnicy jest prosty.
 ∡C=90o jako wpisany oparty na średnicy.
∡C=90o jako wpisany oparty na średnicy.




 hΔ=3
S=(3,0)
(x−3)2+y2=25
y=3 lub y=−3
(x−3)2+9=25⇔(x−3)2=16⇔
x−3=4 lub x−3=−4
x=7 lub x=−1
C1=(−1,3)
C2=(7,3)
C3=(−1,−3)
C4=(7,−3)
hΔ=3
S=(3,0)
(x−3)2+y2=25
y=3 lub y=−3
(x−3)2+9=25⇔(x−3)2=16⇔
x−3=4 lub x−3=−4
x=7 lub x=−1
C1=(−1,3)
C2=(7,3)
C3=(−1,−3)
C4=(7,−3)
 Też tak można.
S − środek AC
Spróbuj tutaj z tw. Pitagorasa
AC2=AB2+CB2
B(x, 5)
Zapisz tu obliczenia, abym widziała, jak to rozwiązujesz.
Już policzyłam.
Też tak można.
S − środek AC
Spróbuj tutaj z tw. Pitagorasa
AC2=AB2+CB2
B(x, 5)
Zapisz tu obliczenia, abym widziała, jak to rozwiązujesz.
Już policzyłam.
 I sposób.
|AC|=√42+122=√16+144=√160=4√10
I sposób.
|AC|=√42+122=√16+144=√160=4√10


 Później to samo w drugim punktem.
Wybacz że się wtrącam, ale też się uczę i czasem staram się pomóc
Później to samo w drugim punktem.
Wybacz że się wtrącam, ale też się uczę i czasem staram się pomóc 
 ( szkoda,że nie chcesz się o nich pouczyć)
( szkoda,że nie chcesz się o nich pouczyć)
 wieje i to bardzo
wieje i to bardzo


 Tak z ciekawości. Dużo czasu dziennie spędzasz na nauce matmy? (dość często Cię tu widzę
Tak z ciekawości. Dużo czasu dziennie spędzasz na nauce matmy? (dość często Cię tu widzę  )
W tym zadaniu które przed chwilą robiłeś bardzo ładne wyniki wychodzą. Ja ogólnie sobie
najpierw rysuje, a później tylko sprawdzam wyniki
)
W tym zadaniu które przed chwilą robiłeś bardzo ładne wyniki wychodzą. Ja ogólnie sobie
najpierw rysuje, a później tylko sprawdzam wyniki 
 Punkty A = (3,1),B = (7,3) są kolejnymi wierzchołkami kwadratu ABCD'
|AB|=√42+22=√20
Prosta AB:
y=ax+b
1=3a+b
3=7a+b
−2=−4a
Punkty A = (3,1),B = (7,3) są kolejnymi wierzchołkami kwadratu ABCD'
|AB|=√42+22=√20
Prosta AB:
y=ax+b
1=3a+b
3=7a+b
−2=−4a



 Myślałem że masz to gdzieś na internecie
Myślałem że masz to gdzieś na internecie 
 Rysujesz parabolę. ( umiesz?)
y = x2 − 6x + 5 =(x−3)2−4
xw=3
yw=−4
x=1 lub x=5
Zadanie bardzo pokrętnie podane.
Chodzi o to, że D i C leżą między miejscami zerowymi.?
OBw=2*|AB|+2*|BC|
D=(xd,0) i C=(xc,0)
xw jest środkiem DC, osią symetrii paraboli jest prosta x=3
Rysujesz parabolę. ( umiesz?)
y = x2 − 6x + 5 =(x−3)2−4
xw=3
yw=−4
x=1 lub x=5
Zadanie bardzo pokrętnie podane.
Chodzi o to, że D i C leżą między miejscami zerowymi.?
OBw=2*|AB|+2*|BC|
D=(xd,0) i C=(xc,0)
xw jest środkiem DC, osią symetrii paraboli jest prosta x=3
