plan
bezendu:
Wykres funkcji f(x)=|x+1| rozcina koło o środku O=(0,0) i promieniu r=5 ma dwie figury. Oblicz
Pole mniejszej z tych figur
Od Pola koła trzeba odjąć to ten obszar nie zakreskowany to wyjdzie, ale jak policzyć ten
obszar
16 mar 21:12
Saizou :
niech rysunek będzie wskazówką
16 mar 21:16
bezendu:
ale ile jest α ?
16 mar 21:18
Saizou : właśnie to trzeba wyliczyć
16 mar 21:19
bezendu:
ale też nie mam i d ?
16 mar 21:22
Saizou :
a 'd' to co to jest?
16 mar 21:23
Mila:
Podpowiedź.
Narysuj cięciwę AB i oblicz pole ΔABC (Δ prostokątny)
A=(4,3)
B=(3,4)
C=(−1,0)
O=(0,0)
Połącz A i O, oraz B i O
Oblicz pole odcinka koła .
16 mar 21:24
Mila:
A=(−4,3)
16 mar 21:26
Saizou : Mila witaj
nie za bardzo dokładna ta podpowiedź ?
16 mar 21:26
Mila:
Mam wykasować?
16 mar 21:28
bezendu:
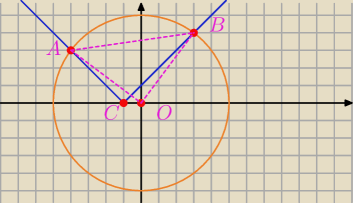
ΔABC jest prostokątny ? Przecież przeciwprostokątna nie jest średnicą tego okręgu ?
16 mar 21:29
Mila:
Prosta y=x+1 jest nachylona pod kątem 45o do osi OX,
a=tgα=1⇔α=45o
∡BCO=45
16 mar 21:33
bezendu:
A trójkąt ACB też jest prostokątny ?
16 mar 21:34
Mila:
Jest, ale to możesz łatwo sprawdzić z tw.odwrotnego do tw. Pitagorasa.
16 mar 21:37
bezendu:
Skoro on jest prostokątny to ja muszę tylko policzyć pole wycinka ?
16 mar 21:40
Mila:
ΔAOB? pytałeś?
16 mar 21:41
bezendu:
Ja pytałem teraz o ΔACB ?
16 mar 21:43
Mila:
Tak 21:33 wyjaśnione. Też możesz sprawdzić z tw.odwrotnego do tw. Pitagorasa.
Wszystkie boki łatwo obliczyć.
ALbo wektory
CA→⊥CB→
16 mar 21:49
bezendu:
Z pola wycinka tak ?
16 mar 21:50
Mila:
Pod=PwycinkaAOB−PΔAOB
Pfigury=PΔACB+Pod
16 mar 21:55
bezendu: czyli pierwszy mój rysunek liczę to zakreskowane ?
16 mar 22:00
Mila:
Tak, ale patrz na rys. 21:29
16 mar 22:18
bezendu:
Tylko nadal upieram się, że wystarczy policzyć pole wycinka bez liczenia pola.
16 mar 22:21
Mila:
Masz odpowiedź do zadania?
16 mar 22:28
bezendu:
Zadanie z arkusza nie mam odpowiedzi
16 mar 22:29
Mila:
Nad AB jest pewien obszar wspólny .
PΔACB≠PΔAOB.
Nie będzie dobrze wg Twojego pomysłu, chyba, że źle Cię rozumiem.
16 mar 22:36
bezendu:
To chyba źle się zrozumieliśmy bo mi chodziło o cały obszar. Dziękuję już sobie poradziłem choć
miałem problem jak wyznaczyć ten kątα
16 mar 22:44
16 mar 22:47
Saizou : najprościej to chyba zauważyć zależność ekierkową (45,45,90) skoro d=5
√2 a r=5
16 mar 22:50
Mila:
A Tobie Saizou jakie wyszło to pole?
16 mar 22:55
Saizou : zaraz przeliczę i powiem
16 mar 22:55
bezendu: również taki, tylko jeszcze muszę poczytać o tym kącie α
16 mar 22:56
Saizou : | | 25 | | 1 | |
mi też wyszło |
| π− |
| |
| | 4 | | 2 | |
16 mar 22:58