1
qu:
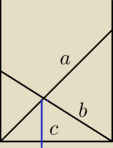
To jest rysunek studni a proste to włożone deski deski
a=3m
b=2m
c=1m
Oblicz średnice tej studni.
16 mar 21:10
Maslanek: Dwa razy Tales i twierdzenie Pitagorasa dwa razy (dla trójkątów najmniejszych)
16 mar 21:51
Maslanek: Może zadziała
16 mar 21:51
qu: to nie jest takie proste
16 mar 22:01
Maslanek: Dwukrotne skorzystanie też bardzo proste nie jest
Nie chciałbym się bawić rachunkami
16 mar 22:04
justi:
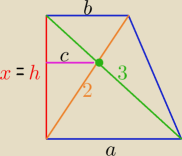
Zauważ trapez prostokątny h−−− średnica studni
| | a*b | |
c= |
| −−− połowa średniej harmonicznej podstaw trapezu |
| | a+b | |
oraz w trapezie prostokątnym
różnica kwadratów długości przekątnych równa jest
różnicy kwadratów długości podstaw a
2−b
2= 3
2−2
2= 5
otrzymasz układ równań:
a
2−b
2=5
następnie z tw. Pitagorasa wyznaczysz
h
i działaj
16 mar 22:49
qu: nie masz podanego ani a ani b patrząc na Twój rysunek
16 mar 22:53
justi:
Nie wiesz,że z układu dwu równań .............. wyznaczysz a i b !
16 mar 22:56
...:
Tyle, że w ten "okrężny" sposób średnicę studni "mierzył" wiejski mądrala.
Twój justi sposób prowadzi do równania stopnia czwartego
17 mar 09:34
tenia:
Podaj zatem, jak by zmierzył tę średnicę "miejski" mądrala
17 mar 12:49
...:
... a w mieście teniu ... nie wiedzą co to studnia ... bo woda jest to to coś co leci z
kranu
17 mar 14:25
Bogdan:
|AE| = |GF| =
√4 − 1 =
√3 i |GB =
√9 − 3 =
√6
| | x+√3 | | x | |
Z podobieństwa trójkątów ABD i EFD otrzymujemy: |
| = |
| ⇒ x = √2 |
| | 1+√6 | | 1 | |
Odp.: Średnica studni =
√3 + p[2}
17 mar 15:54
...:
... oj
Bogdanie ... gdyby średnica miała
√3+
√2 ..., to byłaby większa od 2m
i deska dwumetrowa "rypłaby się" na dno −
17 mar 15:58
Bogdan:
| | 1 | |
bo chochlik się wtrącił i ma być x = |
| , dziękuje za uwagę |
| | √2 | |
17 mar 16:03
Bogdan:
| | x | | √3 | |
Można też wziąć podobne trójkąty DEF i FGB: |
| = |
| |
| | 1 | | √6 | |
17 mar 16:06
...:
... to nie tylko "chochlik" ... źle zinterpretowałeś dane
2 i 3 to długość "całych desek" a nie do punktu przecięcia −
17 mar 16:53
qu: Tak, podane długści to całkowite dł desek.
Żadnych kątów nie ma podanych
17 mar 17:03
Bogdan:
Wziąłem dane wpisane na rysunku qu, a tam odcinek a jest tym, który oznaczyłem BF,
b jest u mnie odcinkiem AF, c to EF.
17 mar 17:09
29 mar 23:04
Mila:
Fantastyczne!
29 mar 23:23