1 qu: Określ dla jakiej wartości parametru m równanie cos2x−cosx=m ma rozwiązanie

Maslanek: cos2x=cos²x−sin²x=2cos²x−1 Więc mamy równanie 2cos²x−cosx−(m+1)=0 Niech t=cos x; t∊<−1, 1> Reszta sam

qu: a co robie z tą m przy liczeniu Δ bo jakoś mi wycohdzi Δ= 9+8m

Maslanek: Musi być rozwiązanie na pewno, więc Δ≥0 Do tego warunki z t

qu: t∊ <−1,1> i co dalej ?

qu: m≥9/8

Mila: f(x)=cos(2x)−cosx f(x)=cos²x−sin²x−cosx f(x)=cos²x−1+cos²x−cosx f(x)=2cos²x−cosx −1 cosx=t , t∊<−1,1> f(t)=2t²−t−1

	1
tw=		∊<−1,1>
	4

Najmniejsza wartość funkcji to

	1
f(		)=...
	4

największą liczysz na końcach przedziału Określisz Zw_f =< ..., ..> oblicz, pytaj, jeśli coś niejasne.

qu: f(1/4) = −9/8 czyli Zwf = <−1,1> bo wierzchołek nie należy do dziedziny ?

Maslanek: Chodziło nam o rozwiązania, wiec zastanówmy się, czy dla t∊<−1, 1> one istnieją Mamy f(−1)=1+1−1=1; f(1)=2−1−1=0 Więc na pewno t=1 jest rozwiązaniem Ale gdzieś między (−1,0) jest jeszcze jedno rozwiązanie.

Maslanek: Ale to wystarczy już tylko podzielić

qu: w zapisach Mili m to tak jakby f(x) ?

Mila:

	1
t=		∊<−1,1>
	4

	1		1		1		−9
f(		)=2*		−		−1=		Najmniejsza wartość funkcji
	4		16		4		8

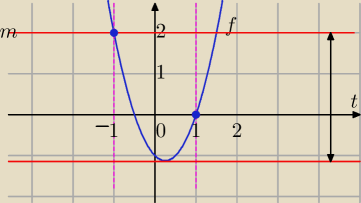
f(1)=2−1−1=0 f(−1)=2+1−1=2 największa wartość f(f) dla t∊<−1,1> równanie

	−9
2cos2x−cosx −1=ma rozwiązanie dla m∊<		,2>
	8

Bo wtedy prosta y=m przecina wykres f(t) w podanych granicach .

qu: Dzięki temu rysunkowi zaczynam to rozumieć Czyli na chłopski rozum mam wierzchołek i wiem , że to jest najmniejsza wartość funkcji potem licz f(1 i −1) i wybieram tą większą liczbę tak to wygląda ?

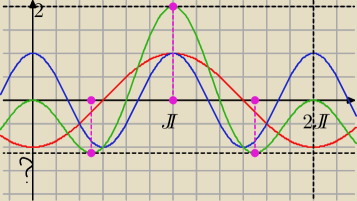
Trivial: Warto znać też interpretację graficzną. Funkcja f(x) = cos(2x) − cos(x) jest sumą funkcji cos(2x) oraz −cos(x). Pytamy o minimum i maksimum funkcji f(x). Maksimum widać od razu − wynosi 2 w punkcie x = π. Z minimum jest gorzej, ale można oszacować, że jest równe około −1.2. Zatem parametr m może przyjmować wartości m∊[?, 2] ≈ [−1.2, 2]. Dokładna odpowiedź wyjdzie przy rozwiązywaniu algebraicznym.

Mila: Zgadza się, już Ci to kiedyś tłumaczyłam. To dobry sposób w wielu przypadkach.

qu: Właśnie przed chwilą odgrzebałem tamten post. Dzięki, może już teraz nie zapomnę