aa hugo:

	x3−7x+6		|f(x)
Naszkicuj wykres funkcji f(x)=		oraz g(x) =		i podaj ich
	x2−3x+2		f(x)

zbiory wartości.

	x3−7x+6		(x−2)(x+3)(x−1)
f(x)=		=		= x+3 ?
	x2−3x+2		(x−1)(x−2)

	|x+3|
g(x)=
	x+3

1) x≥0

x+3
	=1 (f. stała)
x+3

x<0

−x−3
	= −1 (f. stała)
x+3

Suma f(x) i g(x) = {2.4} z założeniem x≠{−3,1,2} Zw={4} dobrze to mam?

...: ... zaczynamy od dziedziny −

hugo: x²+3x+2 ≠0 (x−1)(x−2)≠0 xeR/{1,2} I warunek dla wartości bzwgl po uproszczeniu: x+3 >0 xe(−3o)

...: tego warunku nie ma −

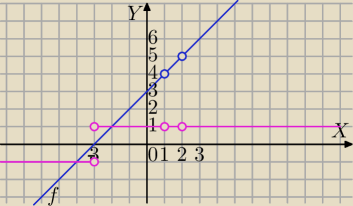
Mila: Porządkujemy informacje.

	x3−7x+6
1) f(x)=
	x2−3x+2

	(x−2)(x+3)(x−1)
f(x)=
	(x−1)(x−2)

D=R\{1,2} f(x)=x+3 Zw_f=R\{4,5}

	|f(x)|		|x+3|
2)g(x)=		=
	f(x)		x+3

D=R\{−3,1,2} g(x)=1 dla x+3>0⇔x>−3 i x∊D g(x)=−1 dla x+3<0⇔x<−3 i x∊D Zw_g={−1,1}

hugo: 1. Nie rozumiem tego 'Zw_f=R{4,5} z czego to wynika? 2. Obliczyłem g(x) = 1 ... i napisałem potem źle i zepsułem sobie rozwiązanie.. mam takie braki 3. Dziękuję !

Mila: f(x)=x+3 po uproszczeniu D=R\{1,2} f(1)=4 f(2)=5 ale odrzucamy te wartości, bo 1,2 ∉D Dlatego ze zbioru wartości f(x)=x+3 odrzucamy {4.5}

hugo: ok ok rozumiem

Mila: