Okrąg o środku w punckie O(-1,2) i promieniu pierwiastek z 10 ma dwa punkty ... gosc: Okrąg o środku w punkcie O(−1,2) i promieniu √10 ma dwa punkty wspólne z prostą AB, gdy: A. A(−3,−3), B(1,−1) B. A(−2,−5), B(2,2) C. A(0,5), B(3,4) D. A(2,1), B (4,7)

5-latek: Jaki jest warunek na to aby prosta miala z okregiem dwa punkty wspolne ?

pog:

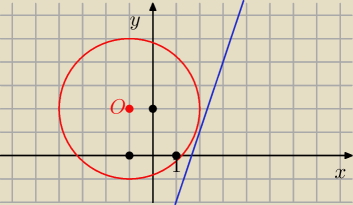
janek191: D) O = ( −1, 2) r = √10 A =(2, 1) B = (4, 7) pr AB : y = 3 x − 5 3 x − y − 5 = 0 Obliczam odległość prostej od środka okręgu

	I 3*(−1) − 1*2 − 5 I		10
d =		=		= √10 = r
	√9 +1		√10

Prosta jest styczna do okręgu.

Mariusz: Równanie prostej dla danych w odpowiedzi A

	−1−(−3)
y−(−3)=		(x−(−3))
	1−(−3)

	1
y+3=		(x+3)
	2

	1		3
y=		x+		−3
	2		2

	1		3
y=		x−
	2		2

(x+1)²+(y−2)²=10

	1		3
y=		x−
	2		2

	1		3
(x+1)2+(		x−		−2)2=10
	2		2

	1		3
y=		x−
	2		2

	1		7
(x+1)2+(		x−		)2=10
	2		2

	1		3
y=		x−
	2		2

	1		7		49
x2+2x+1+		x2−		x+		−10=0
	4		2		4

5		3		13
	x2−		x+		=0
4		2		4

5x²−3x+13=0 9−260 < 0 Prosta nie ma punktów wspólnych z okręgiem Dla pozostałych odpowiedzi sprawdzasz podobnie

Mariusz: 5x²−6x+13=0 Δ=36−260 < 0 ale to niewiele zmienia