Analityczna
Radek:
Dany jest okrąg (x−2)2+(y−1)2=3 . Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
Oprócz okręgu nie mam nic.
16 mar 16:38
5-latek: czyli bedzie okrag opisany na trojkacie
Znajdz sobie wzor na R (promien okregu opisanego na trojkacie rownobocznym
16 mar 16:41
Marcin:
r=
√3
| 2 | |
| h= √3, chyba to  |
| 3 | |
16 mar 16:43
Radek:
| | 2 | |
Już mam  wystarczyło r= |
| h a ja głupi o tym zapomniałem przepraszam |
| | 3 | |
16 mar 16:43
5-latek: lub a=
√3R
| | 1 | | 3 | |
Wtedy P= |
| √3a2= |
| √3R2=3√3r2 |
| | 4 | | 4 | |
r− promien kola (okregu wpisanego )
16 mar 16:50
Radek: Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: P =
(1,3),Q = (− 5,4),R = (− 6,7) ?
16 mar 17:55
Radek: ?
16 mar 18:22
zawodus: znasz wektory?
16 mar 18:31
Radek:
Nie znam wektorów niestety.
16 mar 18:31
Mila:
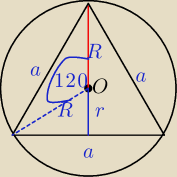
W Twoim zadaniu:
R=
√3
z tego możesz obliczyć a
|| sposób
Pole obliczymy tak:
16 mar 18:41
Radek:
Dziękuję Pani, już tamto policzyłem, chwila słabości
16 mar 18:42
Radek: ?
16 mar 19:10
Radek: ?
16 mar 19:21
Radek: ?
16 mar 20:16
Mila:
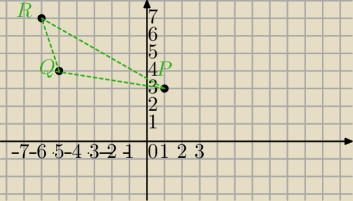
Wektorami najprościej.
P = (1,3),Q = (− 5,4),R = (− 6,7) ?
Bez ektorów to tak:
P jest środkiem AB ( niech A będzie poniżej P)⇔
R jest środkiem BC⇔
Q jest środkiem CA
napisz ostatnie dwa równania i rozwiązuj układ.
16 mar 20:37
Radek:
Nigdy nie lubiłem wektorów i nie jestem ich pewny więc nie chcę ich używać.
16 mar 20:40
Mila:
Musisz się nauczyc. Przecież na fizyce masz wektory.
To nic trudnego i ułatwia rozwiązywanie wiele problemów.
16 mar 20:42
Radek:
Nie wiem czy zdołam opanować, wolę robić arkusze a wiele zadań zrobiłem bez wektorów.
16 mar 20:45
Mila:
Tu jeden wektorek wykorzystam.
QR→=[−1,3]
P(1,3) →T[−1,3]→B=(−1+1, 3+3)
B=(0,6)
P(1,3) →T[1,−3]→A(2,0)
C liczysz wykorzystując, że Q jest środkiem AC
16 mar 20:47
5-latek: Tylko ze Radku na Politechnice Wroclawskiej bolesnie to odczujesz
16 mar 20:50
Radek:
A kto powiedział, że ja idę na politechnikę Wrocławską ?
16 mar 20:53
Radek:
Dziękuję już rozwiązałem bez wektorów
16 mar 20:57