podobieństwo Mary: Z kawałka tektury w kształcie trójkąta ostrokątnego, o podstawie długości 20 cm i wysokości opuszczonej na tą podstawę, równej 12 cm, chcemy wyciąć możliwie największy kwadrat, którego bok zawiera się w podstawie trójkąta. Jaka będzie długość boku kwadratu?

AROB: pomogę

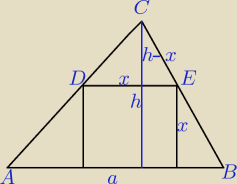
AROB: Ponieważ bok kwadratu DE jest równoległy do podstawy a, to trójkąty ABC i CDE są podobne.

	12 − x		h
Stąd prawdziwa jest proporcja:		=
	x		x

Dane: h=12 cm , a = 20 cm

	12 − x		12
Zatem:		=
	x		20

	12 − x		3
		=
	x		5

3x = 5(12 − x) 3x = 60 − 5x

	60		1
8x = 60 ⇒ x =		= 7
	8		2

	1
Odp. Długość największego boku kwadratu jest równa 7		cm.
	2

Mary: dziękuję bardzo.

Halome: (12 − x) / x = h / x? A nie czasem = h / a ?