proszę bardzo o pomoc. magda.: Na prostej o równaniu 2x−y−5=0. Znajdź punkt,dla którego suma kwadratów jego odległości od osi układu współrzędnych jest najmniejsza

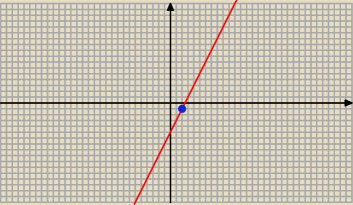
Janek191: P leży na prostej o równaniu y = 2 x − 5, więc P = ( x; y) = ( x ; 2 x − 5) Odległość punktu P od osi OY jest równa IxI , a od osi OX jest równa I 2 x − 5 I Suma kwadratów odległości punktu P od osi jest równa : f(x) = I x I² + I 2 x − 5I² = x² + 4 x² − 20 x + 25 = 5 x² − 20 x + 25

	20
a = 5 > 0 , więc funkcja f posiada najmniejszą wartość dla x = p =		= 2
	10

Wtedy y = 2*2 − 5 = − 1 Odp. P = ( 2; − 1) ==============