przeksztalcenia zadanie: Dla jakiego przeksztalcenia przestrzeni wszystkie wektory sa wektorami wlasnymi dla wartosci

	1
wlasnej		?
	2

wydaje mi sie, ze to bedzie jednokladnosc (J_r(X)=rX)

	1
bo wtedy J1/2(X)=		X
	2

czy dobrze?

zadanie: ?

Trivial: OK.

zadanie: dziekuje

zadanie: mam takie pytanie jezeli mam polecenie: Znajdz wartosci, wektory wlasne i przestrzenie wlasne przeksztalcenia zadanego macierza: 1 −2 −2 −2 1 −2 −2 −2 1 Wyznaczam wartosci wlasne rozwiazujac rownanie charakterystyczne, czyli (1−t)³−8−8−4(1−t)−4(1−t)−4(1−t)=0 −t³+3t²+9t−27=0 −t²(t−3)+9(t−3)=0 (t−3)(−t²+9)=0 t=3∨t=−3∨t=3 czyli wartosci wlasne to: t=−3 oraz t=3. teraz wyznacze wektory wlasne dla tych wartosci wlasnych rozwiazujac rownanie ( T(X)=tX ) dla t=−3: (1 −2 −2) x x (−2 1 −2)*y =−3 y (−2 −2 1) z z x−2y−2z=−3x −2x+y−2z=−3y −2x−2y+z=−3z 4x−2y−2z=0 −2x+4y−2z=0 −2x−2y+4z=0 1^o 2x−y−z=0 2^o −x−2y−z=0 3^o −x−y+2z=0 z 2^o x=−2y−z wstawiam do 3^o −(−2y−z)−y+2z=0 y=−3z to x=5z czyli X=(x,y,z)=(5z,−3z,z)=z(5,−3,1) ; wektorem wlasnym dla t=−3 jest np. (5,−3,1) dobrze sa te obliczenia? prawidlowo wyznaczam te wektory wlasne ? akurat w tym nie wyznaczalem z przyjalem, ze z to z. prosilbym o sprawdzenie

Trivial: Zaraz zerknę.

zadanie: bede czekac

Trivial: Sama metoda wygląda OK, ale zapewne są błędy rachunkowe, bo A[5 −3 1]^T ≠ −3*[5 −3 1]^T. Teraz... Proponuję poznać kilka faktów, które pozwolą sprawdzić poprawność obliczeń, a może nawet znacząco je przyspieszą. (1) Wektory własne macierzy A wyznaczają kierunki, dla których mnożenie przez macierz A działa jak mnożenie przez liczbę. Wektory własne są jedynie skalowane. Ax = λx Dodatkowo, zgadując wektor własny x otrzymamy odpowiadającą λ, mnożąc x przez A. (2) Tr(A) = λ₁ + λ₂ + ... + λ_n Tr(A) = a₁₁ + a₂₂ + ... + a_nn − tzw. ślad macierzy (3) det(A) = λ₁λ₂...λ_n (4) (A−λJ)x = 0 Macierz A−λJ jest osobliwa, czyli można zgadywać λ tak, aby macierz A stała się osobliwa. (5) Wartości własne macierzy symetrycznych (A^T = A) są rzeczywiste, a ich wektory własne mogą zostać wybrane tak, żeby były do siebie prostopadłe. Gdy wszystkie λ są różne, to wektory te na pewno będą prostopadłe. (6) dowolna λ = 0 ⇔ macierz A osobliwa ⇔ detA = 0 (7) każda λ ≠ 0 ⇔ macierz A nieosobliwa ⇔ detA ≠ 0 Odnośnie zadania: 1 −2 −2 A = −2 1 −2 −2 −2 1 Patrząc na macierz A od razu spodziewamy się: (5) Rzeczywistych λ, możliwie prostopadłych x. (4) Parząc na macierz zgadujemy λ₁ = 3, wtedy: −2 −2 −2 A−3J = −2 −2 −2 −2 −2 −2 Macierz jest osobliwa, zatem λ₁ = 3 jest wartością własną macierzy A. Teraz odgadujemy wektor własny x₁. Jaka kombinacja kolumn macierzy A−3J da nam wektor zer? Są dwa niezależne kierunki (dwa liniowo niezależne wektory własne x₁, x₂): 1 0 x₁= −1 x₂ = 1 0 −1 Zatem również λ₂ = 3 (podwójny pierwiastek równania charakterystycznego). (2) λ₁ + λ₂ + λ₃ = Tr(A) = 1 + 1 + 1 = 3 ale znamy już λ₁ + λ₂ = 3 + 3 = 6, zatem λ₃ = 3 − 6 = −3. Wracamy do zgadywania wektora własnego. 4 −2 −2 A+3J = −2 4 −2 −2 −2 4 Jaka kombinacja kolumn macierzy A+3J da nam wektor zer? Po chwili namysłu bez problemu da się zauważyć kombinację: 1 x₃= 1 1 Sprawdzenie. (3) λ₁λ₂λ₃ = det(A) = 1 − 8 − 8 − 8 − 4 − 4 = −27 3*3*(−3) = −27 OK. (5) Macierz symetryczna ⇒ λ rzeczywiste OK.

Trivial: Odnośnie sprawdzenia to pasowałoby jeszcze zobaczyć czy: (5) x₁∘x₃ = 0, x₂∘x₃ = 0 (Natomiast x₁∘x₂ nie musi być zerem, gdyż ich λ była wielokrotna). (1) Ax₁ = 3x₁ Ax₂ = 3x₂ Ax₃ = −3x₃

zadanie: dziekuje

zadanie: wyznacze jeszcze raz te wektory wlasne: 1^o 2x−y−z=0 2^o −x−2y−z=0 3^o −x−y+2z=0 z 1^o 2x−y−z=0 →y=2x−z podstawiam do 3^o wyliczony y: −x−(2x−z)+2z=0 z=x podstawiam do wyznaczonego y=2x−x=x czyli y=x z=x stad: (x,y,z)=(x,x,x)=x(1,1,1) wiec przykladowy wektor wlasny dla t=−3 to (1,1,1) ale rowniez (2,2,2) oraz (3,3,3) itd. dobrze? szczerze mowiac to wole te druga metode z ukladem rownan bardziej ja rozumiem

Trivial: Każda wielokrotność wektora własnego jest wektorem własnym: A(cx) = cAx = cλx = λ(cx). Wektory (1,1,1), (2,2,2), (3,3,3) są w tym samym kierunku, czyli nie wnoszą nic nowego. Proponuję wybrać (1,1,1) gdyż najlepiej wygląda.

Trivial: Na marginesie, metoda "z układem" to dużo więcej pracy. Ja rozwiązywałem ten sam układ, ale zamiast męczyć się z podstawieniami po prostu odgadłem rozwiązanie. Tobie też to polecam − jeśli da się odgadnąć, to próbuj. Jest dużo szybciej. Masz błąd w równaniu 2^o. Ma być +2y.

zadanie: a jakbym teraz mial okreslic przestrzen wlasna to w jaki sposob? przestrzen wlasna moze byc prosta zawierajaca (0,0,0) lub plaszczyzna zawierajaca (0,0,0) lub cala przestrzenia R³. nie wiem czy dobrze rozumiem ale czy przestrzen wlasna to po prostu zbior wszystkich wektorow wlasnych dla danej wartosci wlasnej tzn. np. ze jezeli przestrzenia wlasna bedzie prosta to wektory wlasne sa wlasnie z tej prostej a jezeli bedzie to plaszczyzna to wektory wlasne sa z tej plaszczyzny?

zadanie: tak rzeczywiscie ale na szczescie to nie zmienia odpowiedzi

Trivial: Dla każdej wartości własnej mamy odpowiadającą przestrzeń własną, czyli kombinację liniową wektorów własnych odpowiadającą tej wartości własnej. V_λ1,2 = V₃ = span(x₁, x₂) = { c₁x₁ + x₂x₃ } ← płaszczyzna V_λ3 = V₋₃ = span(x₃) = { cx₃ } ← prosta.

Trivial: V₃ = ... = { c₁x₁ + c₂x₂ }

Trivial: Jeszcze takie ciekawe zadanko na zrozumienie tematu: Bez przeprowadzania żadnych rachunków podać wektory własne macierzy:

	3 0 0 5

Jakie są odpowiadające im wartości własne? Wskazówka: Ax = λx.

zadanie: wartosci wlasne to 3 i 5 bo jest to macierz symetryczna

Trivial: Symetryczna i diagonalna. A wektory własne? Co robi ta macierz? W jakich kierunkach macierz A tylko skaluje wektor x przez λ? (Wtedy x będzie wektorem własnym)

zadanie: wektory wlasne to dla 3 (1,0) a dla 5 to (0,−1) bo sa prostopadle

Trivial: Zgadłeś, ale nie wystarczy żeby wektory były prostopadłe. Na przykład:

	1 1		1 −1

Są prostopadłe, ale nie są wektorami własnymi. Odpowiedz na pytanie: Co robi ta macierz? W jakich kierunkach macierz A tylko skaluje wektor x?

zadanie: no dobrze ale wracajac jeszcze do tamtego zadania dla t=3 mam: z ukladu rownan wyszly 3 takie same czyli: −x−y−z=0 czyli jest to plaszczyzna (przechodzaca przez (0,0,0) i teraz mam podac jej rownanie ogolne i parametryczne ? no to rownanie ogolne to po prostu −x−y−z=0 ? a parametryczne ? a jak wyznaczyc wektory wlasne ? bo jezeli je wyznacze to wtedy napisze rownanie parametryczne tej plaszczyzny bo to beda wektory w nie zawarte

zadanie: pomysle

Trivial: Idąc Twoją drogą musisz wprowadzić dwa parametry − np. y = u, z = v. Wtedy x = −u − v y = u z = v I wybrać dwa niewspółliniowe wektory.

zadanie: obojetnie jakie?

Trivial: Tak, obojętnie jakie. Byle tylko nie były w tym samym kierunku. Proponuję (u,v) = (1,0) i (0,1). Aby otrzymać dokładnie moje odgadnięte rozwiązania podstaw (u,v) = (−1,0), (1,−1).

zadanie: moglbym poprosic o pokazanie bo nie wiem jak

Trivial: Czego nie rozumiesz?

zadanie: czyli mam 2 wektory (−1,0) oraz (1,−1) i teraz podstawiam do rownania: x=−(−1)−0=1 y=−1 z=0 teraz ten drugi: x=−1+1=0 y=1 z=−1 czyli (x,y,z)=(1,−1,0) oraz (0,1,−1) i to sa przykladowe wektory wlasne dla t=3 dobrze?

Trivial: Tak.

zadanie: dziekuje

zadanie: czyli przestrzen wlasna dla t=3 to plaszczyzna. rownanie ogolne tej plaszczyzny to: −x−y−z=0 rownanie parametryczne to: x=−u−v y=u z=v gdzie u i v to niewspolliniowe wektory zawarte w tej plaszczyznie czy tak?

Trivial: Równanie ogólne OK. Można pomnożyć przez (−1). Równanie parametryczne to: [ x ] [−1 ] [−1 ] [ y ] = u [ 1 ] + v [ 0 ] [ z ] [ 0 ] [ 1 ] Gdzie u,v − parametry (liczby). Można też przekształcić to do: [ x ] [ 1 ] [ 0 ] [ y ] = s [−1 ] + t [ 1 ] [ z ] [ 0 ] [−1 ] Gdzie znów: s,t − liczby. To wektory [ −1 1 0 ]^T, [ −1 0 1 ]^T mają być liniowo niezależne. Albo wektory: [ 1 −1 0 ]^T, [ 0 1 −1 ]^T.

zadanie: dziekuje

zadanie: a dla wartosci wlasnej −3 bedzie prosta a jak mam sie zorientowac, ze to bedzie prosta? i podobnie jak z plaszczyzna jak wyznaczyc jej rownanie parametryczne i ogolne?

zadanie: ?

Trivial: 1 wektor opisuje prostą, 2 płaszczyznę, 3 przestrzeń 3D, ...

zadanie: a cos wiecej?

zadanie: dla wartosci wlasnej −3 wektor wlasny to (1,1,1) i teraz jak wyznaczyc przestrzen wlasna dla tej wartosci wlasnej?

zadanie: moge prosic o pomoc?

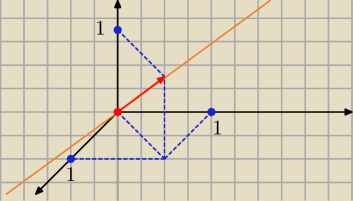
Trivial: No ale co tutaj wyznaczać... Przestrzeń tę tworzą wszystkie wektory postaci c*(1,1,1), czyli prosta.

zadanie: a jakby wygladalo rownanie parametryczne tej prostej?

Trivial: (x,y,z) = c*(1,1,1)...

zadanie: a jak rozpoznac czy jest to prosta czy cała przestrzeń R³?

Trivial: http://pl.wikipedia.org/wiki/Podprzestrze%C5%84_liniowa#Pow.C5.82oka_liniowa

zadanie: mogłbym prosić o bardziej elementarne wytłumaczenie?

Trivial: Nie rozumiesz idei kombinacji liniowej... Nie chcę mi się tego teraz tłumaczyć.

zadanie: to moze pozniej

zadanie: ?