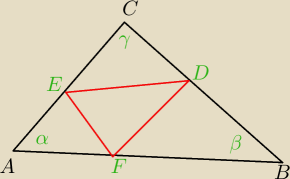
jerey: dany jest trojkat ABC w ktorym ∡BAC = α ∡ABC=β oraz ∡ACB=γ. Na bokach BC, AC i AB tego trójkata wybrano odpowiednio punkty D,E,F w taki sposób, by AE=AF, BD=BF i CD=CE. Wykazac, ze ∡EFD =

	α+β		γ
		=90−
	2		2

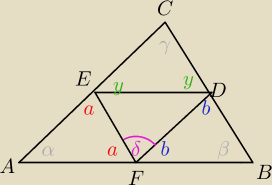Saizou : α+β+γ=180→α+β=180−γ

	180−α
α+2a=180→a=
	2

	180−β
β+2b=180→b=
	2

δ+a+b=180

	180−α		180−β
δ+		+		=180
	2		2

2δ+180−α+180−β=360 2δ=α+β

	α+β		180−γ		γ
δ=		=		=90−
	2		2		2

jerey: dzieki