Ostrosłup Karolka : Dwie ściany boczne ostrosłupa o podstawie trójkąta równobocznego o boku a są prostopadłe do płaszczyzny podstawy, a trzecia ze ścian bocznych tworzy z płaszczyzną podstawy kąt 60 stopni. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

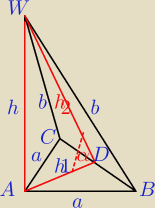
Janek191: α = 60^o

	√3
h1 = a
	2

−−−−−−−−

h		√3		3
	= tg α = tg 60o = √3 ⇒ h = √3*h1 = √3*a		=		a
h1		2		2

h = 1,5 a −−−−−−−−

	√3
h22 = h2 + h12 = (1,5 a)2 + [ a		]2 = 2,25 a2 + 0,75 a2 = 3 a2
	2

więc h₂ = √3 a −−−−−−−− Objętość ostrosłupa

	1		1		a2 √3		1		√3
V =		Pp*h =				*h =		a2 √3*1,5 a =		a3
	3		3		4		12		8

====================================== Pole powierzchni całkowitej

	a2√3
Pc = Pp + 2 P1 + P2 =		+ 2* 0,5 a*h + 0,5 a*h2 =
	4

	a2√3		a2√3
=		+ a*1,5 a + 0,5 a*√3 a =		+ 1,5 a2 + 0,5√3 a2 =
	4		4

	√3a2		6 a2		2 √3 a2		(3√3 + 6 ) a2
=		+		+		=
	4		4		4		4

===============================