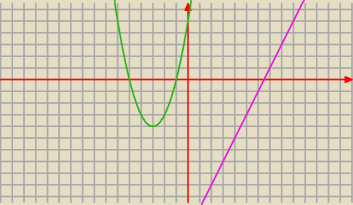
g Radek: 1. Na paraboli o równaniu y = x²+6x+5 znajdź współrzędne punktu A , którego odległość od prostej o równaniu y = 2x−13 jest najmniejsza. I dalej co mam robić ? Czy to będzie wierzchołek tej paraboli

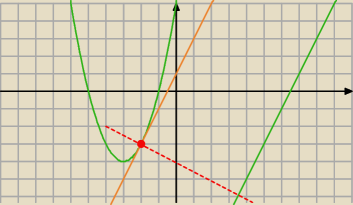
wredulus_pospolitus: tym punktem będzie punkt dla którego styczna do tej paraboli jest równoległa do tejże prostej y=2x−13 pytanie brzmi −−− czy potrafisz wyznaczyć równanie stycznej

Bogdan:

Radek: a) czemu akurat ten punkt ? b) proszę mi pokazać na innym przykładzie jak wyznaczyć styczną do paraboli

wredulus_pospolitus: poziom liceum Styczna o równaniu y=ax+b układ równań: y=x²+6x+5 y = 2x + b będzie miało dokładnie jedno rozwiązanie 2x + b = x²+6x+5 x² + 4x + (5−b) = 0 'to ma mieć jedno rozwiązanie' Δ = 4² − 4(5−b) =0 (aby było jedno rozwiązanie) stąd: b = 1 x = −2 y = −3 punkt ma współrzędne (−2,−3) natomiast styczna dana jest równaniem y=2x+1 liczysz odległość pomiędzy prostymi i koniec zadania

Radek: Ja jestem w liceum 3 klasa.

Radek: Dziękuję

Radek: Ale właściwie czemu mam liczyć długość odcinka skoro można wyznaczyć punkt styczności ?

zawodus: punkt na paraboli ma współrzędne (x,x²+6x+5)

	|Ax+By+C|
d=
	√A2+B2

szukasz minimum d

Radek: ?

zawodus: wredulus potrzeba uzasadnienia dlaczego szukasz stycznej do wykresu... czytałeś mój pomysł?

Radek: Tak, ale analizuję rozwiązanie wredulusa. I pytam czemu mam liczyć długość odcinka skoro ten punkt styczności mam ?

Mila: Z definicji odległości punktu P(x,y) od prostej y=2x−13⇔2x−y−13=0 postac ogólna. P(x,y)=(x,x²+6x+5) punkt leżący na paraboli

	|2x−x2−6x−5−13|
d=g(x)=
	√22+12

	|−x2−4x−18|		|x2+4x+18|
g(x)=		⇔g(x)=
	√5		√5

g(x) ma najmnieszą wartość w wierzchołku paraboli Δ<0 funkcja przyjmuje tylko wartości dodatnie, a najmniejszą w weirzchołku tej paraboli

	x2+4x+18
g(x)=
	√5

x_w=−2 obliczymy jaka wartość ma f(x) dla x=−2 f(−2)=4+6*(−2)+5=9−12=−3 P=(−2,−3) szukany punkt.

zawodus: nie musisz liczyć jego współrzędnych, ale musisz uzasadnić, że ten punkt będzie tym którego poszukujemy

Radek: Ale jak to uzasadnić ?

Radek: ?

Radek: ?

Mila: Dlaczego nie przeanalizujesz sposobu z 21:46, taki częściej się stosuje w LO.

Radek: Analizuję, ale tamten również chcę zrozumieć

Radek: Pani sposób rozumiem, bo pokazywała mi Pani już kiedyś jak pisać styczne

Mila: To dobrze.

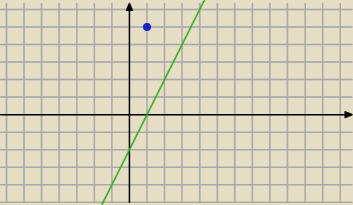
Radek: 2/ Jeden z boków kwadratu ABCD jest zawarty w prostej o równaniu 2x−y−2=0 . Wierzchołek A ma współrzędne (1,5) . Znajdź współrzędne pozostałych wierzchołków Tutaj wyjdą dwa rozwiązania, prawda ?

Mila: Tak w górę po prostej i w dół.

Radek: A jak Pani jest na forum to mam pytanie odnośnie zadania z arkusza zadania.info 2 w tym zadaniu z geometrii analitycznej też wyjdą dwa rozwiązania ? Poziom R

Mila: W którym zadaniu? W 8?

Radek: Tak

Mila: Jutro rozwiążę, to odpowiem.

Radek: Dobrze, to jeszcze proszę o wskazówki do pozostałych zadań z geometrii analitycznej

Radek: 3/ Wierzchołki A i B kwadratu ABCD leżą na paraboli 2 y = x − 6x + 19 , przy czym odcinek AB jest równoległy do osi Ox . Wykaż, że jeżeli odległość punktu A od osi Ox jest liczbą całkowitą to pole kwadratu ABCD również jest liczbą całkowitą.

Mila: No co z tym zadaniem, robisz coś? Podpowiedź. y=x²−6x+9 przyjmuje tylko wartości dodatnie. x= A(a,b) b− odległość A od osi OX.

Radek: Nie wiem jak dokonczyć

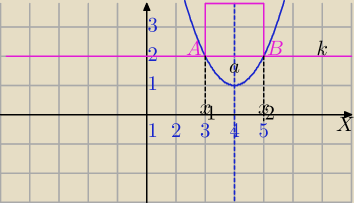
Mila: Szkic paraboli (innej dla c=10) prosta AB jest równoległa do OX, odległość Prostej od osi Ox jest liczbą całkowitą P_□=a² a=|(x₂−x₁)|=x₂−x₁ dla x₂>x₁ f(x₁)=f(x₂)=k⇔ x²−6x+19 =k x²−6x+19−k=0 P_□=(x₂−x₁)² rozwiń i przedstaw w postaci, aby można skorzystac z wzorów Viete'a

Radek: Połowy z tych zadań nie rozumiem, bo są dla mnie bardzo trudne.

Mila: Skąd bierzesz te zadania? To jest trudne zadanie.

Radek: Z arkuszy z poziomu R. To może na początek łatwiejsze ? Jednokładność ?

Mila: Skończ tamto. Zrób co Ci poradziłam. Jakoś dobrniemy do końca.

Radek: P=x₂²−2x_x2+x₁² P=(x₁+x₂)²−4x₁x₂

Mila: x₁+x₂=6 x₁*x₂=19−k Podstaw i odpwiedz na pytanie. To znaczy czy tak obliczone pole jest liczba całkowitą?

Radek: 6²−4(19−k) 36−76+4k P=−40+4k ?

Mila: No i zbadaj czy spełniony jest warunek : −40+4k>0

Radek: 4k>40 k>10

Mila: Co to znaczy w tym zadaniu i czy możliwe spełnienie.

Radek: K jest większe od 10 ?

Mila: x_w=3 f(3) =10 najmniejsza wartość funkcji. Prosta równoległa ma przecinać wykres, czyli leży nad wierzchołkiem i wtedy k>10, co oznacza, że P>0 Koniec.

Radek: Chyba zajmę się innymi zadania z tej analitycznej a te zostawię na następny weekend