plani bezendu: Udowodnij, że jeżeli środki boków dwóch czworokątów wypukłych pokrywają się, to pola tych czworokątów są równe.

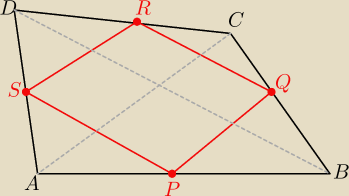
Mila: P,Q,R,S− środki boków czworokąta ABCD. 1) Wykaż, że : P_ABCD=2*P_PQRS (Pan Tales pozdrawia) Potem wnioski.

zawodus: narysuj rysunek

zawodus: Witam MiLA wystarczy podobieństwo

bezendu: Ja bym się tu nigdy Talesa się nie spodziewał.

Mila: Jak zwał tak zwał. Odcinek łączący środki boków Δ jest równoległy do boku trzeciego i równy jego połowie. Masz Δ podobne, gdzie ? Spojrzyj uważnie.

bezendu: ΔDOC i ΔAOB ΔDOA i ΔBOC

Mila: Przeczytaj 20:57.

bezendu: Czytałem i Twierdzenie Talesa.

Mila: AC||RS i AC|| PQ i wtedy masz podobne Δ.

Mila: No i co wykazane?

bezendu: Nie do końca jeszcze.

bezendu: Już chyba mam, teraz muszę wrócić do brył bo to zadania którego nie rozwiązałem chodzi mi po głowie cały czas

Mila: Widzę, że tracisz precyzję.

bezendu: Chyba tak.

bezendu: Wykaż, że istnieją dokładnie dwie liczby naturalne n takie, że trójkąt o bokach n ,n+ 2,n + 3 jest rozwartokątny. Z twierdzenia cosinusów i wychodzi n=2 lub n=3 OK ?

Piotr 10: lub też tak (n+3)² > n²+(n+2)² n∊N

Piotr 10: n² − 2n − 5 > 0 Δ_n=24 √Δ_n=2√6 n₁=1+√6 ; n₂= 1 − √6 √6≈2,45 n∊( − ∞ ; 1 − √6 ) ∪ ( 1 + √6 ; +∞ ) ∧ n∊N n={2;3} ok

bezendu: To nie wiem po co ja tam tw cos wykorzystywałem Dzięki, nie musiałeś pisać rozwiązania

Piotr 10: Chciałem policzyć, a kartki nie chciało mi wyciągać się

Mila: Bezendu obydwa sposoby dobre, ale trzeba wypisać trójki boków i odrzucić jedną. Piotr masz błąd. Szukaj.

Piotr 10: Jakoś nie widzę błędu, trójkąt o bokach 2; 4 ;5 oraz 3 ;5 ;6 istnieje

Piotr 10: Czy po prostu błąd w rachunkach ?

Marcin: Piotr: n∊(1−√6; 1+√6) n∊N

Mila: n²−2n−5<0 i n∊N₊ n∊{1,2,3} po sprawdzeniu, z jakich odcinków można zbudować Δ, masz dobrą odpowiedź.

Piotr 10: a ok