pierwiastki szopa: Dla jakich wartosci parametru m rownanie |x² − 2mx| = 1 ma trzy rozne pierwiastki?

wredulus_pospolitus: na dwa przypadki i rozwiązujesz

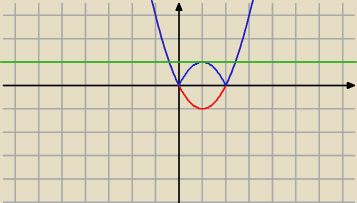
MQ: Można te z wykombinować: Z rysunku widać, że będzie to wtedy, gdy wierzchołek będzie miał wsp. y = −1

MQ: Miało być: Można też wykombinować: Z rysunku widać, że będzie to wtedy, gdy wierzchołek paraboli x²−2mx będzie miał wsp. y = −1

pigor: ..., lub analitycznie może np. tak : dane równanie |x²−2mx|=1 ⇔ x²−2mx=1 v x²−2mx=−1 ⇔ x²−2mx−1=0 v x²−2m+1= 0, to, aby ta alternatywa "dala" 3 różne pierwiastki Δ₁=4m²+4>0, więc już mamy ∀m∊R zapewnione 2 różne pierwiastki, to jeszcze jeden ⇔ Δ₂=0 ⇔ ⇔ 4m²−4=0 ⇔ m²=1 ⇔ |m|=1, a stąd i z m∊R ⇔ m∊{−1,1} . ...