Oblicz długość odcinka łączącego punkty styczności. walt: Z punktu A=(17,16) poprowadzono styczne do okręgu o równaniu (x+3)²+(y−1)²=125. Oblicz długość odcinka łączącego punkty styczności. S=(−3,1) r=5√5 y=ax+b 16=17a+b b=16−17a y=ax+16−17a ax−y+16−17a=0

	|−3a−1+16−17a|		|−20a+15|
d=		=		=5√5
	√a2+1		√a2+1

|−4a+3|=√5√a²+1 /² (−4a+3)²=5(a²+1) 16a²−24a+9=5a²+5 11a²−24a+4=0 Δ_a=576−176 √Δa=20

	2
a1=
	11

a₂=2

	2
y1=		x+b
	11

y₂=2x+b Czy do tego momentu jest ok? Nie mam pomysłu co dalej zrobić ...

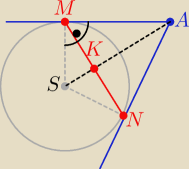
Eta: Proponuję tak: 1/ wyznacz długość |SA| 2/ wyznacz długość |MA| z tw. Pitagorasa w ΔSMA 3/ z tw. o odcinkach stycznych : |MA|=|NA| 4/ długość wysokości |MK| poprowadzonej z wierzchołka kąta prostego w trójkącie SMA :

	|SM|*|MA|
|MK|=		=.......
	|SA|

to |MN| = 2*|MK|= ...... i to wszystko

Eta: w/g powiedzenia : " rozwiązać zadanie każdy może, ale najprostszą drogą.. tylko nieliczni mogą" pozdrawiam

walt: Eta, zanim wrzuciłem to zadanie na stronę to spojrzałem na odpowiedzi w internecie po czym znalazłem Twoje rozwiązanie, jest prostsze to prawda Czy jednak mógłby ktoś pomóc mi w moim rozumowaniu? Jest ono w ogóle właściwe?

walt: up

walt: up