prosze o pomoc trygometria Monika: trygometria pilne prosze o pomoc Monika: Mój problem to trygometia nie było mnie na zajęciach właśnie wtedy i niestety samej nie udaje mi sie tego rozwiązać prosze o pomoc z góry dziękuje : 1)α jest kątem ostrym i sin α=4cos α ,oblicz sin α oraz cos α 2)α jest kątem ostrym i 3sin α=5cos α ,oblicz tg α oraz ctg α 3)wiedząć ze sin α=0,8 i α∊(0stopni ,90stopni).Wykaż ze dla dowolnego konta ostrego α dane wyrazenie równa się tg α przez cos α 4)oblicz wartość wyrazenia pierwiastek z sin kwadrat 27stopni + sin kwadrat 63stopnie przez 4 5)oblicz wartość wyrażenia cos kwadrat 40stopni + cos kwadrat 50stopni + cos kwadrat 60stopni Przeprasza za taki zapis niestety nie potrafie inaczej

5-latek:

	sin27+sin2 63
4)		=
	4

sin63=sin(90−63)=cos27

	sin2 27+cos2 27
to		= policz co mamy w liczniku ?
	4

Monika: jeden

Janek191: 1) sin α = 4 cos α / : cos α

sin α
	= tg α = 4
cos α

	y		4
tg α =		=		⇒ x = 1 i y = 4
	x		1

zatem r² = x² + y² = 1² + 4² = 1 + 16 = 17 r = √17 więc

	y		4		4√17
sin α =		=		=
	r		√17		17

	x		1		√17
cos α =		=		=
	r		√17		17

Monika: a skąd te r x i y

Janek191: 2) 3 sin α = 5 cos α / : 3

	5
sin α =		cos α / : cos α
	3

sin α		5
	= tg α =
cos α		3

więc

	1		3
ctg α =		=
	tg α		5

Monika: i czy dobrze odpowiedziałam 5 latkowi na pytaie ile jest w liczniku

Monika: czy te litery r x y to zamiast sinus cosinus ?

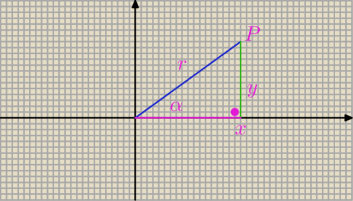
Janek191: P = ( x; y) r² = x² + y²

	y		x		y		x
sin α =		cos α =		tg α =		ctg α =
	r		r		x		y

Janek191: Tak, bo sin²α + cos² α = 1

Monika: czyli wynik bedzie jedna czwarta tak ?

Monika: a mogła bym prosić jeszcze o 5zadanie i bardzo dziękuję za wytłumaczenie i pomoc

Janek191:

	√ sin2 27o + cos2 63o
Tam jest		?
	4

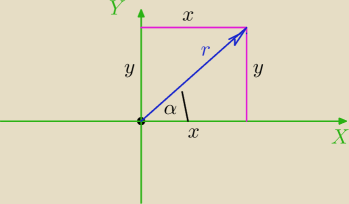
5-latek: Taki sam rysunek masz w swojej ksiazce r− to promien wodzacy( nasza przeciwprostokatna)

	x
z definicji cosinusa cos alfa =
	r

z definicji sinusa ze jest to stosunek przyprostokatnej lezacej naprzecieko kata do

	y
przeciwprostokatnej mamy sinalfa =
	r

I dobrze i odpowiedzialas . W liczniku mamy jedynke trygonometryczna

5-latek: Janek juz Ci wytlumaczyl

Janek191: 5) cos 50^o = cos ( 90 − 40)^o = sin 40^o

	1
cos 60o =
	2

zatem cos² 40^o + cos² 50^o + cos² 60^o =

	1		1		1
= cos2 40o + sin2 40o + (		)2 = 1 +		= 1
	2		4		4

Janek191: W z.3 coś brakuje !

J:

	sin227 + cos263		sin227 + cos2(90−27)
4) √		= √		=
	4		4

	sin227 + 1 − sin227		1		1
√		= √		=
	4		4		2

Monika: tak tam właśnie było ze stopniami i w pierwiastku odp do wypowiedz z godz 9:45

Monika: Oj faktycznie 3 zle napisałam to miało być tak : Wiedząc że sin α=0,8 i α∊(0stopni,90stopni),oblicz pozostałe wartośći funkcji trygometrycznych kąta α

Monika: a i takiego rysunku nie miałam bo to sa same zadania z trescia na kartce

J:

	√sin227 + sin263		√sin227 + sin2(90 −27)		√sin227 + cos227
4)		=		=		=
	4		4		4

	√1		1		1
		=		, a jeśli 4 było pod pierwiastkiem to wynik:
	4		4		2

Monika: 4 jest w mianowniku i pierwiastek odnosi sie do calosci

J: sinα = 0,8 cosα = √1 − sin²α = √1 −0,64 = √0,36 = 0,6

	sinα		0,8		4		1		3
tgα =		=		=		, ctgα =		=
	cosα		0,6		3		tgα		4

Monika: tam jest 90 −27 a 5latek napisał ze to jest 90−63

J: Pomylił się: sin63 = sin(90−27) = cos27

Monika: a jezeli jest ze Tangens kąta ostrego α jest równy pierwiastek z dwóch przez pierwiastek z 3 oblicz sin α

Monika: aha dziękuję

5-latek: oczywiscie ze ma byc 90−27 (moja pomylka

5-latek: Czesc J Dobrze ze poprawiles

J: Cześć ... ja też sie pomyliłem, wczesniej

Monika: a na tym obrazku do zadania pierwszego co oznacza to Duze P

Monika: dziękuje wam za pomoc jak dobrze że są tacy ludzie na świecie którzy służą pomoca!

J: To jest punkt na ruchomym ramieniu kąta.

Monika: a jezeli jest ze Tangens kąta ostrego α jest równy pierwiastek z dwóch przez pierwiastek z 3 oblicz sin α miała być jeszcze ostatnią prośbę pomocy w tym zadanku

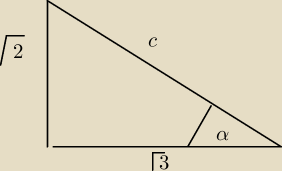
5-latek: do postu z 11:13

	tgx
Albo policzysz ze wzoru ze sin x =
	√1+tg2x

lub popatrz na rysunek

	√2
tgalfa =
	√3

	√2
Z twierdzenia pitagorasa oblicz c a sin alfa =
	c

J:

	sin2x		2		2
Albo ...		=		⇔ 3sinx = 2(1 − sin2x) ⇔ 5sin2x = 2 ⇔ sinx = √
	cos2x		3		5

5-latek: Ja jednak mysle ze MOnika bedzie studentka i jeszce jej napisze ze jesli ma podany tg to

	1
to cos x=		)
	√1+tg2x

Monika: Staram sie nauczyć ,i zawsze ta strona stoji mi pomocą .Ostatnio uczyłam sie z tej strony logarytmów analizowałam teorie i wszystkie przykłady i dostałam 5

J: No to gratulacje

Monika: a mógłbyś mi pokazać jak to powinno wyglądać bo ja sie zawsze na podstawie przykładów ucze jezeli nie mam zadznym zrobionych na których moge sie zasugerować

Monika: w poscie z godz 9:58 jest w równaniu 1 a w poscie z godz 11 nie ma To które rozwiązanie jest prawidłowe

J: Post 9:58 nie traktuj, pomyliłem się. Dobre rozw. jest post 11:00

Monika: OK dziękuje wam za pomoc