wykresy funkcji kwadratowej z wartością bezwzględną Robaczek: Jak się rysuje takie wykresy jak: |x²−4|+3x=y x|x−4|=y Próbuje i za nic nie wychodzi..

bartymeusz: musisz obliczyć miejsca zerowe, funkcji w module i zbadać, gdzie są ujemne gdzie dodatnie, w tych przedziałach gdzie są ujemne opuszczając moduł ,znaki wyrazu + na − −na + wyrażeń pod modułem

Robaczek: a jak to zatem narysować? Jakiś prosty przykład.

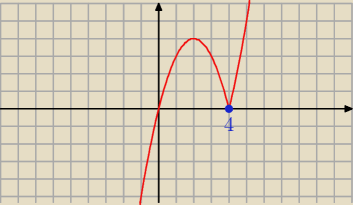
5-latek: to jest wykres y=x|x−4| rysujesz go tak . Patrzysz i widzisz ze modul sie zeruje dla x=4 teraz dla x<4 |x−4|=−(x−4)=−x+4=4−x wiec dla x<4 funkcka bedzie miala postac y=x(4−x)=4x−x² Natomiast dla x>=4 |x−4|=x−4 wiec w tym przedziale funkcja bedzie miala postac y=x(x−4)=x²−4x Wiec rysujesz wykresy tych funkci ale tylko w wyznaczonych przedzialach

Robaczek: |x2−4|+3x=y x²>=4 x>=2 Zatem dla x>=2 wartość bezwzględna się zeruje i będzie wyglądała tak: x²−4+3x=y <2,+nieskończoność) A dla x<2 −x²+3x+4=y (−nieskończoność,2) Dobrze?

Robaczek: Widzę mój błąd, w pierwszym (−niesk.,−2><2,+niesk.) W drugim (−2,2) Wybaczcie, godzina nie moja.

5-latek: Teraz dobrze . Wiec idz spac i rano wroc do zadania

Robaczek: No dobrze, ale rysując go za nic nie mogę zrobić tego jak tutaj jest https://www.wolframalpha.com/input/?i=%7Cx2%E2%88%924%7C%2B3x

Robaczek: Zrozumiałem tamto + zrobiłem kilka następnych zadań. Jednakże pojawił mi się kolejny problem: Wyznacz wszystkie takie wartości parametru k ∈ R , aby liczba 2 znajdowała się między miejscami zerowymi funkcji f(x) = x 2 + 4x + k. Dlaczego f(2)<0, nie rozumiem tego. Rozumiem to, że funkcja niekoniecznie musi mieć wierzchołek w x=2, ale dlaczego to?

Robaczek: I dlaczego w tym zadaniu 5.18 Znajdz te wartosci parametru m dla których funkcja f(x) = x2 + mx + 9 ma dwa miejsca zerowe większe od 2. uwzględniami warunek f(2)>0? Jak ma się to do zadania?

Robaczek: Może o tej godzinie ktoś zdoła odpowiedzieć na moje pytania

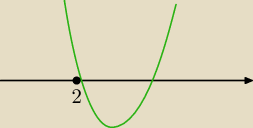
J: Aby obydwa pierwiastki były większe od 2 , to: 1) wierzchołek paraboli musi leżeć na prawo od x = 2 2) wartoścć f(2) > 0

Robaczek: Tyle to ja też wiem, ale nie wiem dlaczego wartoścć f(2) > 0 takie coś, skąd to się wzieło. Ja tego nie widzę.

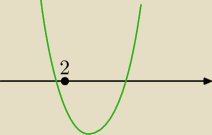
J: Bez 2−go warunku mogłoby być tak:

Robaczek: A jak to zobaczyć, skąd to wynika?

J: I na drugim rysunku f(2) < 0

wredulus_pospolitus: Robaczek ... jeżeli f(2) = 0 ... to w x=2 mamy miejsce zerowe (sprzeczne z treścią zadania) jeżeli mamy f(2) < 0 ... to oznacza, że (skoro ramiona skierowane do góry) jedno miejsce zerowe jest mniejesze od x=2, a drugie jest większe stąd warunek f(2) > 0 gwarantuje nam że ALBO oba miejsca zerowe będą większe od x=2 ALBO oba będą mniejsze od x=2

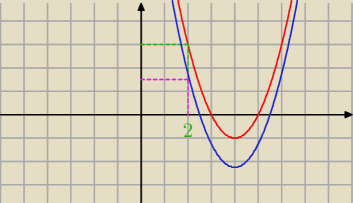
Aga1.: Ramiona paraboli skierowane do góry

J: Popatrz dobrze na te dwa rysunki. jeżeli pierwiastek leży na lewo od 2 (czyli jest mniejszy od dwóch) to cały czas f(2) < 0 , gdy f(2) = 0 to x jest dokladnie równe 2, a gdy f(x) > 0 , to pierwiastek leży na prawo od 2, czyli jest wiekszy od 2.

wredulus_pospolitus: a tak wprowadzając trochę zamętu −−− ten warunek NIE JEST konieczny, ponieważ możemy sobie znakomicie poradzić używając wzorów Viete'a

Robaczek: A mógłbyś pokazać to na wzorze Viete'a?

wredulus_pospolitus: chociaż nie ... cofam te swoje głupoty o wzorach Viete'a

Robaczek: wredulus_pospolitus: Czyli te twoje 3 warunki trzeba zapamiętać, czy da się jakoś do tego dojść? Po samym rysunku nie widzę tego, tzn. widzę zależności wyżej, ale sam bym do tego nie doszedł, że f(2)>0

wredulus_pospolitus: Robaczek ... 'te moje warunki' to jest po prostu opisanie obserwacji. Narysuj sobie parę paraboli z ramionami skierowanymi do góry i patrz jaka jest zależność pomiędzy f(2), a miejscami zerowymi, które funkcja posiada