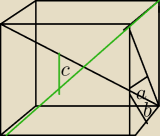
ll jolene1310: oblicz katy a, b, c w szescianie, wynik podaj w zaokragleniu do pelnych stopni odp to a 35 b 55 c 70

jolene1310: ?/

pigor: ..., niech krawędź sześcianu ma długość 1, to z tw, cosinusów :

	34+34−1		12		1
cos(c)=		=		=
	2*12√3*12√3		32		3

więc cos(c)= 0(3) ⇒ c= 70^o. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1√2
cos(a)=		= 13p{6] ⇒ a= 35o
	1√3

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1
cos(b)=		⇒ cos(b)= 13√3 ⇒ b= 55o . ...
	1√3

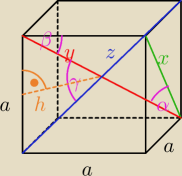Domel: x = a√2

	a		a		1		√2
tgα =		=		=		=		=> α = 35°
	x		a√2		√2		2

y = z = √a² + x² = √a² + 2a² = √3a² = a√3

	y		z
γ − kąt wierzchołkowy trójkąta o bokach a,		i
	2		2

	a		y
Trójkąt dzielimy na 2 trójkąty prostokątne o bokach		,		i h
	2		2

γ

a

y

a

2

a

a

1

sin

=

:

=

*

=

=

=

2

2

2

2

y

y

a√3

√3

	γ		√3		γ
sin		=		=>		= 35° => γ = 70°
	2		3		2

Jak widzisz kąt β przesunąłem w inny narożnik − ale to ten sam kąt co u ciebie. Można go wyznaczyć na 2 sposoby: I° W trójkącie o bokach a, x i y znamy kąty α i 90° − a suma kątów w trójkącie wynosi 180° 180° = 90° + α + β => β = 90° − α = 90° − 35° = 55° lub z tangensa

	x		a√2
tgβ =		=		= √2 => β = 55°
	a		a