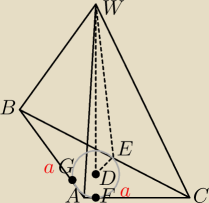
 |<BAC| = 90o
D − spodek wysokości
Rysunek może nie najlepszy, ale okrąg jest styczny do boków podstawy ostrosłupa w takich
punktach E, F, G, że punkty styczności E, F, G z wierzchołkiem W ostrosłupa tworzą wysokości
ścian bocznych. Co za tym idzie.
r = |GD|=|ED|=|FD|
h = |WD|
Powstają trzy trójkąty prostokątne ΔEDW, ΔDFW, ΔDGW. Mając r, h z Pitagorasa łatwo wyliczyć,
że:
|GW|=|EW|=|FW|, czyli te trójkąty są przystające do siebie a to oznacza, że
|<DFW|=|<DEW|=|<DGW| są takie same, czyli ściany boczne są nachylone do podstawy pod takim
samym kątem.
Aby obliczyć tangens nachylenia ściany bocznej do (krawędzi podstawy?). Może płaszczyzny
podstawy miało być? W każdym razie i tak za mało danych bo wysokość mogę zmieniać dowolnie i
tangens będzie też się zmieniał.
|<BAC| = 90o
D − spodek wysokości
Rysunek może nie najlepszy, ale okrąg jest styczny do boków podstawy ostrosłupa w takich
punktach E, F, G, że punkty styczności E, F, G z wierzchołkiem W ostrosłupa tworzą wysokości
ścian bocznych. Co za tym idzie.
r = |GD|=|ED|=|FD|
h = |WD|
Powstają trzy trójkąty prostokątne ΔEDW, ΔDFW, ΔDGW. Mając r, h z Pitagorasa łatwo wyliczyć,
że:
|GW|=|EW|=|FW|, czyli te trójkąty są przystające do siebie a to oznacza, że
|<DFW|=|<DEW|=|<DGW| są takie same, czyli ściany boczne są nachylone do podstawy pod takim
samym kątem.
Aby obliczyć tangens nachylenia ściany bocznej do (krawędzi podstawy?). Może płaszczyzny
podstawy miało być? W każdym razie i tak za mało danych bo wysokość mogę zmieniać dowolnie i
tangens będzie też się zmieniał.
| a2 | a | |||
r = | = | |||
| a*( 2 + √2) | 2 + √2 |
| h | h | ||||||||||||
tg α = | = | ||||||||||||
| r |
|
| 2 + √2 | ||
tg α = | * h | |
| a |