1 qu: f(x)= (sinx+cosx)² jak to zacząć ?

Radek: sin²x+2sinxcosx+cos²x

Marcin: f(x)=sin²x+2sincos + cos²x f(x)=2sinxcosx+1 f(x)=2sin2x+1 Może jakoś tak?

qu: i z tego 1+2sinx cosx ?

Utem: f(x)=2sinx cosx+1 f(x)=sin(2x)+1 I o co Ci chodzi? Nie napisałeś polecenia.

Marcin: Ja się oczywiście poprawiam i usuwam tą 2 w ostatnim zapisie (omyłkowo ją tam wklepałem)

qu: określ zbiór wartości tej funkcji

Utem: To już proste f(x)=sin(2x)+1 Zacznij samodzielnie, sprawdzę.

qu: nie za bardzo pamietam czym się rózni sinx od sin2x i co to zmienia w obliczeniach

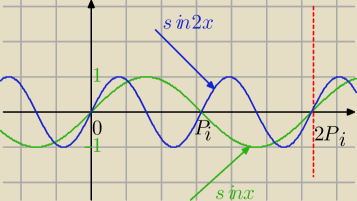
Utem: Jak widać obie funkcje mają taki sam zbiór wartości. −1≤sin(2x)≤1 /+1 0≤sin(2x)+1≤2 Z_wf=<0,2>

qu: OK a jak by było 2sinx to by była 2x rozciągnięta w górę czyli y (−2,2 ) ?

Utem: 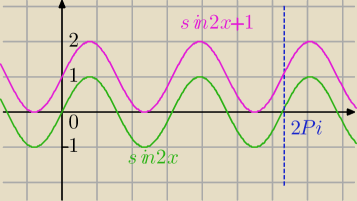f(x)=sin(2x)+1

Utem: g(x)=2sinx (wykres y=sinx rozzciągnięty w górę i w dół) Z_w=<−2,2>

qu: o to mi właśnie chodziło ogólnie to w zadaniach ze zbiorem wartości to muszę minimalny y i maksymalny y tak ? tylko jak mam funkcję kwadratową z trygonometryczną to jak jest dodatnia to liczę wierzchołek który jest minimalnym y a maksymalny to jest z dziedziny danej funkcji ? o to mniej więcej chodzi ?

Utem: Wierzchołek musi byc z dziedziny, wtedy wartość będzie najmniejsza dla paraboli skierowanej do góry i wartość największa dla paraboli skierowanej w dół.

qu: czyli np jak mam wierzchołek −2 to liczę przy standardowym cosx f(−1) i f(1) to to bedzie zbiór wartości ?

qu: a gdy wierzchołek należy do dzieciny to biore wierzchołek czy w przypadki funkcji ramionami do góry f(−1) ?