1 qu: f(x)− sinxcosx

	1
p=
	2

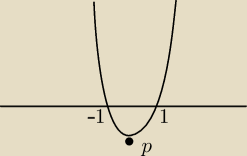
f(−1)= −2 f(1)=0 patrze na wirzchołek p i to jest najmniejsza wartość a największa to któraś z f(−1) i f(1) ? czyli 0 tak to się parzy

	1
y∊<		; 0 > ?
	2

Utem: Napisz porządnie treść zadania.

qu: określ zbiór wartości funkcji f(x)= sinxcosx

Utem:

	1
f(x)=		sin(2x) [ ze wzoru: sin(2α)=2sinα*cosα ]
	2

Spróbuj samodzielnie zacząć.

qu: a mogę zrobić to bez tego wzoru czyli f(x) = −sin²x +sinx podstawiam t=sinx i wychodzi f(t)= −t² +t ?

Utem: No , ale ta funkcja 22:02 skąd się wzięła? To nowe zadanie?

qu: to to samo tylko jakoś to zroibłem ..... f(x)= sinxcosx f(x)= sinx(1−sinx) f(x)= −sin²x +sinx

Mila: No to całkiem źle to zrobiłeś. Pomyliło Ci się z jedynką trygonometryczną. cos²x=1−sin²x

qu: faktycznie ogarnąłem już to ze wzoru i wyszło właśnie

1
	sin2L
2

1/2 czyli funkcja spłaszczona 2x a sin2L nie wpływa na wartość funkcji czyli y∊<−1/2, 1/2> zgadza się teraz?

Mila: Tak.

qu: dziękuje