r qu: wyznasz zbiór wartości f(x)= sin²x*cos⁴x+sin⁴*cos²x f(x)= sin²x*cos²x (cos²x + sin²x) f(x)= sin²x*cos²x f(x) = sin²x *(1−sin²x) f(x)= sin²x−sin⁴x sin²x = t dobrze myśle ?

ZKS: Lepiej zrobić tak

	1		1
sin2(x)cos2(x) =		* 4sin2(x)cos2(x) =		* [2sin(x)cos(x)]2 =
	4		4

1
	sin2(2x).
4

Eta:

	1
f(x)= sin2x*cos2x =		sin2(2x)
	4

qu: skąd ta ¹₄

Eta: 2sinx*cosx=sin(2x)

	1		1
to		*(2sinx*cosx *2sinx*cosx)=		sin2(2x)
	4		4

ZKS:

	1
A ile to jest		* 4?
	4

qu: nie ogarniam dokończe jeszcze tak jak to chiałem wcześniej zrobić. f(x)= −sin⁴x +sin²x sin²=t f(t)= −t² +t p(wierzchołek) − od tego momentu nie rozumiem za bardzo co i jak wiem, że tak trzeba

	1
p=
	2

f(−1) = 0 f(1) = 0

	1		1
f(		) =
	2		4

wiem ze trzeba to obliczyć tyle że nie wiem jak odp ogarnąć i po co to liczę

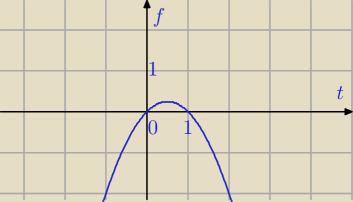
Mila: f(x)=−sin⁴x+sin²x sin²x=t, t∊<0,1> f(t)=−t²+t

	1
tw=		∊<0,1> zatem największa wartość funkcji to
	2

	1		1
f(		)=
	2		4

f(0)=0 f(1)=0 0 to wartość najmniejsza f(x)

1
	to największa wartość funkcji f(x)
4