11 qu: znajdz najmniejszą i największą wartość funkcji f(x) = −cos²x − 4cosx+5 po wszelakich obliczeniach wierzchołek paraboli wychodzi mi −2 f(1) = 8 f(−1) = 0 x należy od <−1,1> tylko nie wiem dlaczego nie ma o −2 do 8 (taka odp) skoro wierzchołek paraboli to −2

ZKS: Widziałeś kiedyś żeby cos(x) = −2?

qu: a 8 może być ?

ZKS: Widzę że brakuje podstaw. Wynik 8 to jest wartość funkcji f(x).

qu: może od początku mam obliczyć maksymalny y i minimalny y tak ? podstawowy cos należy <−1, 1> ale dalej to nie czaje tego

ZKS: U Ciebie nie x ∊ [−1 ; 1] tylko cos(x).

qu: mam prośbę Mógłbyś napisać słowami co mam zrobić w tym zadaniu aby je dokończyć ? od momentu gdy wyszło mi f(x)= −t² − 4t+5 bym był bardzo wdzięczny

Mila: t=cosx, |t|≤1 f(t)= −t²−4t+5 i t∊<−1,1> to jest dziedzina f(t)

	4
tw=		=−2∉<−1,1>
	−2

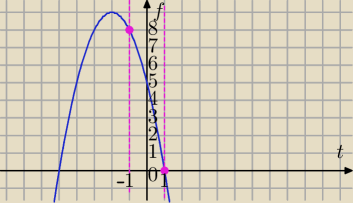
W takim razie funkcja jest monotoniczna w przedziale <−1,1> Wartość największą i najmniejszą szukasz na krańcach dziedziny⇔ f(−1)=−1+4+5=8 f(1)=−1−4+5=0 8>0 8 to wartość największa w przedziale <−1,1> 0 to wartość najmniejsza w przedziale <−1,1>

qu: dzięki, dużo już mi się rozjaśniło czyli wierzchołek przydałby się tylko gdyby należał do <−1,1 > a gdybym miał wyznaczyć do tego zbiór wartości funkcji to y należy od (nie wiem od kąd) do 8 tak ?

Utem: Zbiór wartości f(x): Z_w=<0,8> ( od najmiejszej do największej wartości.)

qu: tak myślałem tylko jeszcze jednego nie wiem dlaczego −2 nie może być bo nie należy do dziedziny t ?

Utem: Napisałam Ci w drugiej linijce 21:00.