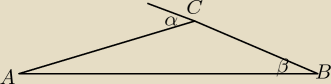
geeoometriaa Ergo: Zadanie proste ale geometrii nie rozumiem często. Bardzo proszę, żeby ktoś mi dokładnie co i jak wytłumaczył. Dany jest trójkąt ABC, w którym |∡β|=β, a kąt zewnętrzny przy wierzchołku C ma miarę α. Wykaż,że jeśli α=2β, to trójkąt ABC jest równoramienny.

tim: Ja spróbuję pomóc.

Ergo: okej będę wdzięczny jeśli wytłumaczysz mi to jak tłumanowi

tim: BAC γ ACB δ ABC β δ = 180 − α β + γ + δ = 180 β + γ + 180 − α = 180 β + γ − α = 0 β + γ = α Więc, jeżeli α = 2β, a β + γ = α, to γ = β i trójkąt jest równoramienny.

tim: BAC γ ACB δ ABC β δ = 180 − α β + γ + δ = 180 β + γ + 180 − α = 180 β + γ − α = 0 β + γ = α Więc, jeżeli α = 2β, a β + γ = α, to γ = β i trójkąt jest równoramienny.

Eta: Miara kata zewnętrznego w trójkacie = sumie miar kątów wewnętrznych do niego nie przyległych więc < CAB = β wiec trójkat jest równoramienny o ramionach: IACI= IBCI lub dokładniej tak: kąt ACB = 180^o −α to: <CAB = 180^o −(β+180^o −α) = α − β= 2β−β=β zatem < CAB = <CBA= β czyli trójkat jest równoramienny

Eta: Miara kata zewnętrznego w trójkącie = sumie miar kątów wewnętrznych do niego nie przyległych więc < CAB = β wiec trójkat jest równoramienny o ramionach: IACI= IBCI lub dokładniej tak: kąt ACB = 180^o −α to: <CAB = 180^o −(β+180^o −α) = α − β= 2β−β=β zatem < CAB = <CBA= β czyli trójkat jest równoramienny

tim: Eta.. mógłbym na słowko ponownie?

Eta: Nie wiem czemu poszły aż dwa wpisy ? Wszystko przez ten "ukochany" Rzeszów

Eta: A na trzy słówka ? może być? ...... timuś

Ergo: heh politechnika Rzeszowska?

Eta: UR (dawne WSP) .. (mat− fiz)

tim: Eta już się nie uczy.... Jakbyś nie wiedział. Eto zapraszam do pokoju zwierzeń.

Ergo: wiem, bo napisała, że studiowała w Rzeszowie