pla
bezendu:
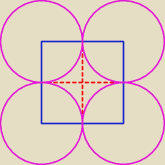
Z wierzchołków kwadratu o boku a , jako ze środków zakreślono 4 okręgi o promieniu a2 . Znajdź
promienie okręgów stycznych do tych czterech okręgów jednocześnie.
Co mam teraz zrobić ?
12 mar 18:48
Eta:
| | a√2 | | a | |
r1(małego stycznego wewnątrz w rozecie) = |
| − |
| =... |
| | 2 | | 2 | |
| | a | |
r2 ( dużego stycznego na zewnątrz do wszystkich kół) = 2* |
| +r1=.. |
| | 2 | |
i tyle
12 mar 18:58
bezendu:
Dziękuję. Zrozumiałem
12 mar 19:01
Eta:
można też tak:
12 mar 19:06
12 mar 19:07
bezendu:
Ostatni mój wpis źle
12 mar 19:14
bezendu:
No właśnie r
2 połowa przekątnej+promień okręgu
12 mar 19:16
bezendu:
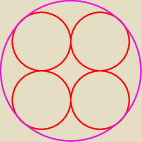
W okrąg o promieniu x wpisano w sposób symetryczny cztery przystające okręgi.
Taki rysunek do zadania ?
12 mar 19:21
Mila:
Tak.
12 mar 19:42
bezendu: W okrąg o promieniu 6 cm wpisano w sposób symetryczny cztery przystające okręgi. Oblicz ich
promień
6−2r ?
12 mar 20:01
Mila:
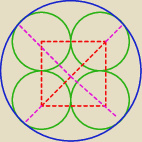
Połącz środki małych okręgów i patrz po przekątnej.
12 mar 20:37
bezendu:
12 mar 20:41
Mila: r− promień małego koła
Przekątna kwadratu o boku 2r
d=2r√2
6−r=?
12 mar 20:47
bezendu:
√2r ?
12 mar 20:49
Mila:
Dobrze
6−r=r√2
12 mar 21:02
bezendu:
To już mam, ciężko mi idą tę okręgi. Dziękuję
12 mar 21:05
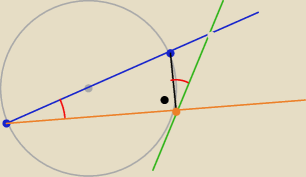
bezendu: Z punktu A leżącego na okręgu poprowadzono średnicę AB i cięciwę AC , które tworzą kąt o
mierze 20∘ . Przez punkt C poprowadzono styczną do okręgu przecinającą prostą AB w punkcie
D . Oblicz miary pozostałych kątów trójkąta ACD .
Mi wychodzi, że to jest 700
12 mar 21:36
Utem:
A mnie 50o i 110o. Mam Ci to rozrysować?
12 mar 21:41
bezendu:
Tak proszę, bo nie wiem czemu moje odp jest niepoprawna.
12 mar 21:42
Eta:
70 i 110
12 mar 21:45
bezendu:
110 ?
12 mar 21:45
Eta:
50 i 110
12 mar 21:46
Eta:
12 mar 21:53
bezendu:
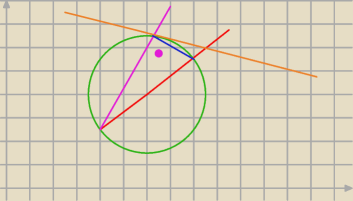
to wychodzi 70
12 mar 21:57
Utem:
Jasne, czy jeszcze objaśniać ?
Tam masz kąt dopsany równy wpisanemu o mierze 20.
90o+20o=110 w pomarańczowym wierzchołku.
12 mar 21:58
bezendu:
Jeszcze objaśnić.
12 mar 22:01
Eta:
Co objaśnić?
12 mar 22:05
bezendu:
czemu tam jest 50 a nie 700 tak jak w moich obliczeniach
12 mar 22:08
Eta:
|<ACD|=20
o +90
o= 110
o ( suma kata dopisanego i prostego
|<DAC|=20
o to |<ADC|= 180
o−(20
o+110
o)= ........
12 mar 22:11
Eta:
Może u Ciebie suma kątów w trójkącie =
200o ?
12 mar 22:13
Utem:
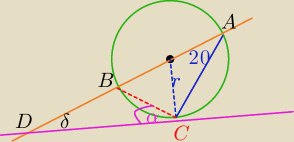
BC cięciwa
∡BCA=90
o jako wpisany oparty na średnicy.
α− kąt między styczną a cięciwą jest równy kątowi wpisanemu opartemu na tej cięciwie (20
o)
∡DCA=90
o+20
o=110
o
δ=180
0−(20
o+110
o)=50
o
12 mar 22:13
Eta:
12 mar 22:14
Eta:
Idę sobie
bo "Mila" aż się pali do rozwiązywania !
12 mar 22:15
bezendu:
Dziękuję teraz już zrozumiałem w końcu.
12 mar 22:16