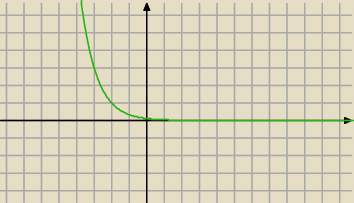
matura Paulina: Wracam jeszcze do wykresów Dziś miałam takie coś na maturce i nie zrobiłam niestety Wykres ten przekształcono w symetrii środkowej względem punktu (1,− 1) , a następnie w symetrii osiowej względem prostej x = − 2 . Otrzymano w ten sposób wykres funkcji g(x) = b ⋅a^x + c . Wyznacz liczby a,b,c i naszkicuj wykres funkcji y = g(x ) .

Mila: Miałaś podany wzór funkcji, której wykres narysowałaś?

Paulina: Nie, sama doszła w domu do wykresu ale nie wiem jak to zrobić tak jak w pleceniu funkcja jest malejąca więc a<1

Mila: Przecież, aby dokonać przekształceń, to muszę wiedziec co mam przekształcać, podaj w całości oryginalną treść zadania.

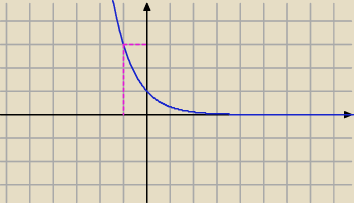
Paulina: Na rysunku przedstawiono wykres pewnej funkcji wykładniczej f(x) = a^x dla x ∈ R . Wykres ten przekształcono w symetrii środkowej względem punktu (1,− 1) , a następnie w symetrii osiowej względem prostej x = − 2 . Otrzymano w ten sposób wykres funkcji g(x) = b⋅a^x+c . to jest oryginał

Mila: 1) ustal wzór funkcji podanej wykresem i wzorem ogólnym f(x)=a^x

Paulina:

	1
y=		x
	3

Mila:

	1
f(x)=(		)x funkcja wykładnicza.
	3

	1
y=(		)x
	3

S(1,−1) − środek symetrii x'=−x+2*1⇔x'=−x+2 y'=−y+2*(−1)⇔y'=−y−2 współrzędne punktu po przekształceniu. ⇔ x=−x'+2 y=−y'−2

	1
podstaw do wzoru y=(		)x i oblicz y'
	3

Paulina: A mogę wiedzieć skąd te znaczki ? prim ?

Mila: To nie miałaś wyprowadzanych wzorów i Pani dała na próbnej?

Paulina: Miałam ale ja pamiętam tylko przekształcenia −f(−x) |f(x)| f(−x) i translacja o wektor. Pisałam, że wykresy funkcji idą mi słabo.

pigor: ... , widzę to tak : mianowicie z wykresu odczytuję, że może to być wykres funkcji wykładniczej malejącej y=a^x i 0<a<1 i a⁻¹=3 ⇔ a= ¹₃ ⇒ y= (¹₃)^x i teraz w symetrii środkowej S_(1,−1)(x,y)=(2*1−x,2*(−1)−y)= (2−x,−2−y) mamy −2−y=(¹₃)^2−x ⇔ y= −(¹₃)^2−x−2 ⇔ y= −¹₉*(¹₃)^−x−2 ⇔ ⇔ y= −¹₉*3^x−2 i dalej w symetrii osiowej względem prostej x= −2 , czyli w S_{x= −2} (x,y)= (−x−2,y) mamy y= −¹₉*3^−x−2−2= = −¹₉*¹₉*3^−x−2 , czyli g(x)= −¹₈₁* (¹₃)^x−2 − szukany wzór, a więc (a,b,c)= ( ¹₃,−¹₈₁,−2) − szukane liczby a,b,c . ... −−−−−−−−−−−−−−−−−−−−−−−−−−− choć głowy nie dam sobie za to wszystko ... uciąć

Paulina: + te które Ty mi ostatnio pokazałaś.

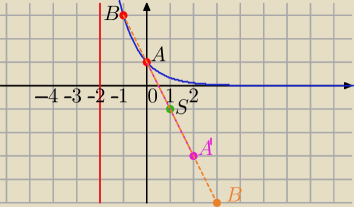
Mila: No nie rozumiesz o co pytam. Wrócimy do tego. Inaczej rozwiążemy. Ponieważ masz podany ogólny wzór funkcji wynikowej g(x)=b*a^x+c to zrobimy tak. 1) Masz dwa punkty wykresu A(0,1) i B=(−1,3) Znajdujemy punkty symetryczne do A i B względem punktu S. A'=(2,−3) (algebraicznie znajdujesz z własności, że S jest środkiem AA', potrafisz?) B'=(3,−5) Teraz prosto dalej. 2) Znajdź punkty symetryczne do A' i B' wględem prostej x=−2 i podaj.

Paulina: algebraicznie to każdy potrafi A'=(−6,−3) B'=(−7,−5)

Mila: A"=(−6,−3), B"=(−7,−5) te punkty należą do wykresu funkcji g(x). Teraz podstaw współrzędne tych punktów do wzoru

	1
y=b*(		)x+c i rozwiąż układ równań.
	3

Zapisz tutaj obliczenia.

Paulina:

	1
b*(		)6{−6}+c=−3
	3

	1
b*(		)−7+c=−5
	3

b*3⁶+3=b*3⁷+5

	1
b=−
	729

Mila: Dobrze.

	1
b=−(		)6
	3

	1		1
−3=−(		)6*(		)−6+c
	3		3

−3=−1+c c=−2 ⇔

	1		1
g(x)=−(		)6*(		)x−2
	3		3

Ten sposób chyba zrozumiałaś.

Paulina: Tak, dziękuję tylko z tym miałam problem.