dowód
Walek: Uzasadnij, że dla k=2 równanie | |x−2| − x| = k ma nieskończenie wiele rozwiązań
11 mar 19:21
Kejt:
||x−2| −x | = 2
|x−2| − x = 2 v |x−2| −x = −2
|x − 2| = 2 + x v | x − 2 | = −2 + x
itd.
powinny wyjść równania tożsamościowe
11 mar 19:23
Walek: wychodzą równania typu −4 = 0 / 2x = 0....
11 mar 19:23
Kejt: pokaż jak liczysz
11 mar 19:24
...:
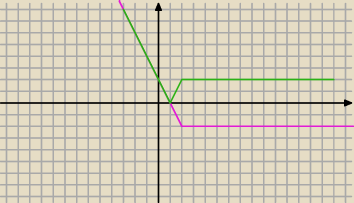
11 mar 19:29
Walek: x − 2 = 2 + x lub x − 2 = − 2 − x....... , jak inaczej mam liczyć?
11 mar 19:31
wredulus_pospolitus:
1) niech x≥2
wtedy |x−2| = x−2
więc | |x−2| − x| = |x − 2 − x| = |−2| = 2
jak widzisz ... masz nieskończenie wiele rozwiązań
11 mar 19:38
Walek: wielke dzięki wredeluspospolitus
11 mar 19:40
