 Geometria płaska− trojkąty.
W trójkącie ABC poprowadzono dwusieczną kąta przy wierzchołku A, która przecięła bok BC w
punkcie D. Wiedząc, że |AC|=|AD| i |AB|=|BC|, oblicz kąty trójkąta ABC.
Geometria płaska− trojkąty.
W trójkącie ABC poprowadzono dwusieczną kąta przy wierzchołku A, która przecięła bok BC w
punkcie D. Wiedząc, że |AC|=|AD| i |AB|=|BC|, oblicz kąty trójkąta ABC.
| 1 | ||
|∡DAC|= | α stąd mamy równanie: | |
| 2 |
| 1 | ||
α+α+ | α=180 stad mamy: | |
| 2 |

 ale przyznam szczerze, że nadal nie wiem skąd to się wzięło...kompletnie nie wiem
jak mam to zapisać
ale przyznam szczerze, że nadal nie wiem skąd to się wzięło...kompletnie nie wiem
jak mam to zapisać
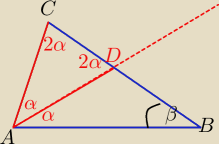 ∡A=2α , kąt został podzielony na dwa kąty równe α dwusieczną AD→
∡A=∡C=2α, bo ΔABC jest Δ równoramiennym z treści zadania
∡D=∡C=2α, bo ΔACD jest Δ równoramiennym z treści zadania
2α+2α+α=180o suma kątów w ΔADC
5α=180o
α=36o
∡A=∡C=2α=2*36o=72o
∡B=180o−2*72o=36o
∡A=2α , kąt został podzielony na dwa kąty równe α dwusieczną AD→
∡A=∡C=2α, bo ΔABC jest Δ równoramiennym z treści zadania
∡D=∡C=2α, bo ΔACD jest Δ równoramiennym z treści zadania
2α+2α+α=180o suma kątów w ΔADC
5α=180o
α=36o
∡A=∡C=2α=2*36o=72o
∡B=180o−2*72o=36o