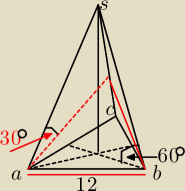
 Dany jest ostrosłup prawidłowy trójkątny. Krawędź podstawy ostrosłupa jest równa 12, krawędź
boczne jest nachylona do płaszczyzny podstawy pod kątem o mierze 60.
a) wyznacz pole przekroju ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i
nachyloną do niej pod kątem o mierze 30.
b) wyznacz cosinus kąta ściany bocznej przy podstawie tego ostrosłupa.
Mam problem ze zrobieniem rysunku, mógłby ktoś na to spojrzeć?
Dany jest ostrosłup prawidłowy trójkątny. Krawędź podstawy ostrosłupa jest równa 12, krawędź
boczne jest nachylona do płaszczyzny podstawy pod kątem o mierze 60.
a) wyznacz pole przekroju ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i
nachyloną do niej pod kątem o mierze 30.
b) wyznacz cosinus kąta ściany bocznej przy podstawie tego ostrosłupa.
Mam problem ze zrobieniem rysunku, mógłby ktoś na to spojrzeć?
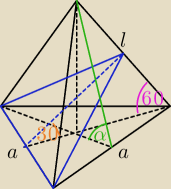 a = 12
a = 12
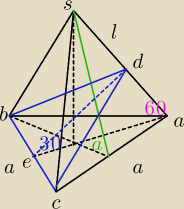
| a√3 | ||
|AE|=h= | =6√3 | |
| 2 |
| 1 | ||
P= | *|DE|*12 | |
| 2 |
| |DE| | ||
cos30= | ||
| h |
| √3 | ||
6√3* | =|DE| | |
| 2 |
| 1 | ||
P= | *9*12=54 | |
| 2 |
| 1 | a√3 | ||||||||||
oblicz krawędź boczną l z cosinusa | = cos 60o = | hp = | ||||||||||
| l | 2 | 2 |
