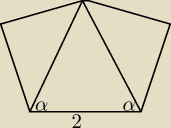
 Schemat okna składającego się z trzech trójkątów równoramiennych:jednego dużego i dwóch małych
przystających.Podstawa dużego trójkąta ma długość 2. Oznamczamy kąty przy podstawie tego
trójkąta przez α. Ramiona dużego trójkąta są jednocześnie podstawami dwóch małych trójkątów.
Kąty przy podstawach małych trójkątów są równe α/2.
a)Wyznacz kąt α, dla którego suma pól małych trójkątów jest równa połowie pola dużego trójkąta
Błagam
Schemat okna składającego się z trzech trójkątów równoramiennych:jednego dużego i dwóch małych
przystających.Podstawa dużego trójkąta ma długość 2. Oznamczamy kąty przy podstawie tego
trójkąta przez α. Ramiona dużego trójkąta są jednocześnie podstawami dwóch małych trójkątów.
Kąty przy podstawach małych trójkątów są równe α/2.
a)Wyznacz kąt α, dla którego suma pól małych trójkątów jest równa połowie pola dużego trójkąta
Błagam 
| 1 | α | α | ||||
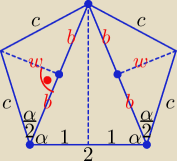
Połowa pola dużego trójkąta = | *1*2b*sinα = b*2sin | cos | ||||
| 2 | 2 | 2 |
| 1 | α | α | ||||
Suma pól małych trójkątów = 4* | bc*sin | = 2bcsin | ||||
| 2 | 2 | 2 |
| α | α | α | α | α | ||||||
2bsin | cos | = 2bcsin | ⇒ c = cos | ⇒ c2 = cos2 | ||||||
| 2 | 2 | 2 | 2 | 2 |
| b | α | b | α | |||||
oraz | = cos | , | = c ⇒ b = c2 ⇒ b = cos2 | |||||
| c | 2 | c | 2 |
| 1 | α | |||
W dużym trójkącie: | = cosα ⇒ 1 = 2*b*cosα ⇒ 1 = 2*cos2 | *cosα | ||
| 2b | 2 |
| α | ||
Uwzględniając tożsamość: 2cos2 | = 1 + cosα otrzymujemy równanie: | |
| 2 |