funkcja wykładnicza tweety: Zbadaj liczbę rozwiązań równania |2^|−x+1|+1 − 4| = m² − 2 w zależności od wartości parametru m (x i m należą do R) Najlepiej jakby ktoś rozwiązał graficznie. Proszę o pomoc

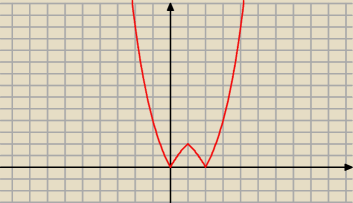
Maslanek: Czerwony − lewa strona

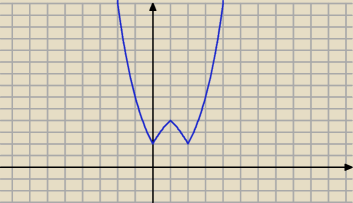
Maslanek: Albo jeszcze lepiej y=|2^|−x+1|+1−4|+2 − niebieski Wtedy potrzebujesz rozwiązań równania y=m².

tweety: dzięki, a lewa mogę tak, czy inna kolejność? L= |2^{|−x+1| +1} − 4| f(x)=2^x → wykres f(x+1) = 2^x+1 → wykres 1 w lewo f(|x|) = 2^|x|+1 →wykres: lewa zmienia się w prawa f(−x) = 2^|−x|+1 → zamiana lewej z prawa f(x+1) = 2^{|−x +1|+1} → wykres 1 w lewo f(x) −4 = 2^{|−x +1|+1} − 4 → wykres 4 w dol |f(x)| = |2^{|−x +1|+1} − 4| → odbijam dolna czesc do góry

tweety: aa no i jeszcze +2 na koniec czyli 2 do gory

Lala: tak sie doczepie bo ciekawe zadanie, co później z tym y=m²?

pigor: m²= const, czyli rysujesz sobie proste y= const= m² równoległe do Osi Ox "idąc" od dołu i tak : 0 rozwiązań ⇔ y=m²< 2 ⇔ |m|< √2 ⇔ −√2< m< √2 ⇔ [c[m∊(−√2;√2); 2 rozwiązania ⇔ y=2 v y>4 ⇔ m²=2 v m²>4 ⇔ |m|=p{2| v |m|>2 ... itd. 3 rozwiązania ⇔ y=4 ⇔ m²=4 ⇔ |m|=2 ⇔ ... itd. 4 rozwiązania ⇔ 2< y< 4 ⇔ 2< m²< 4 ⇔ √2< |m|< 2 ⇔ ... itd. ...

Maslanek: f(−x) = 2^|−x|+1 → zamiana lewej z prawa f(x+1) = 2^{|−x +1|+1} → wykres 1 w lewo Ta druga linijka się nie zgadza. Przesuwamy jeden w prawo. Mamy f(x−1)

tweety: @pigor a nie mogę narysować obu w układzie wsp i odczytac i prawą strone narysować tak jak wyżej (ta parabola)? @Maslanek a nie ciągle w lewo, skoro chce mieć |−x+1|, czyli − −1, czyli translacja o [−1,0] ?

pigor: ..możesz też o samo "robić" z czerwonym wykresem; ale wtedy "bawisz się" prostą y=m²−2 na tym wykresie .

Maslanek: W prawo Weźmy f(x)=−x Wtedy po translacji o T[1,0] mamy: f(x−1)=−(x−1)=−x+1

tweety: rozumiem, dzięki