wielomiany like: 2x³−2x²−18x+18≥Ix²−9I

Wazyl: Definicja wartości bezwzględnej zawsze ratuje (podziel na przedziały).

like: 2x³−2x²−18x+18≥x²−9 v 2x³−2x²−18x+18<9−x² 2x³−3x²−18x+27≥0 v 2x³−2x²−18x+9<0 (2x−3)(x−3)(x+3)≥0 v (2x−1)(x−3)(x+3)<0 x ∊<−3,3/2>u<3,∞) v x∊(−∞,−3)u (1/2,3)

Wazyl: Podstaw −100000. Jeżeli w zadaniu masz "x" poza wartością bezwzględną to niebezpiecznie stosować sposób: |coś|=1 |coś|=1 v coś=−1

like: to jak to lepiej zrobić?

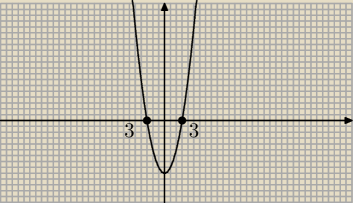
Wazyl: Po lewej ma byc −3. Czyli dla przedziału (−3;3) Wyrażenie w wartości bezwzględnej przyjmuje wartości ujemne. Zatem rozwiązujesz nierówność w tym przedziale a opuszczając wartość zmieniasz znaki. Potem rozwiązujesz dla dodatnich wartości i wtedy już nie zmieniasz znaku

like: czyli że dla x∊(−3,3) 2x³−2x²−18x+18<− x²+9 czy 2x³−2x²−18x+18<x²−9?

like: ...

Wazyl: Górne!

like: wyszło mi tak jak wczesniej napisałam z 1) x∊ {−3} u <3,∞) z 2) x∊ (1/2,3) z 2) cos mam zle

Wazyl: Wyszło inaczej W zbiorze rozwiązań nie masz −100000

like: to co skopalam?

Wazyl: Nie mam obliczeń więc nie wiem. Widzę tylko że chyba odp jest zła: jeżeli robisz założenie x∊(−3;3) to liczą się TYLKO te liczby. Czyli jak odp wyjdzie: <−1;5> tzn prawidłowa odp <−1;3)! "Zawężasz" swój "świat" liczb do (−3;3) Potem rozwiązujesz dla R\ (−3;3) . Przykład wychodzi Ci x∊R \{−100}. Odp Brzmi: x∊(−∞;100)U(−100;−3>U<3;+∞) rozumiesz ?

like: obliczenia mam na samej gorze a potem wlasnie zawęzałam biorac pod uwagę zalozenia, odp z książki to x∊<−3,1/2> u <3,∞)

Wazyl: Drugi przedział źle przerzuciłeś "x²" na drugą stronę.