geometria kartezjańska thebestnickintheweb: Okrąg o środku w punkcie (2,2) przechodzi przez początek układu współrzędnych i jest styczny do prostej k w punkcie S = (a,4), gdzie a > 0. Wyznacz równanie prostek k.

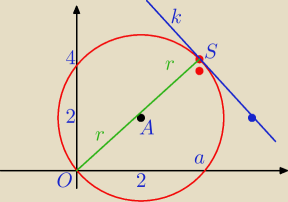
Janek191: A = ( 2; 2 ) S = ( a; 4) , a > 0 r = I A O I = 2√2 ⇒ r² = 8 ( x − 2)² + ( y − 2)² = 8 Prosta OA y = a x 2 = 2 a ⇒ a = 1 y = x ==== Prosta k jest prostopadła do prostej OA, więc y = − x + b i jest styczna do danego okręgu x² − 4 x + 4 + ( − x + b − 2)² = 8 x² − 4 x + 4 + x² − 2*( b − 2) x + b² − 4 b + 4 = 8 2 x² − 4 x − 2 b x + 4 x + b² − 4 b = 0 2 x² −2b x + b² − 4 b = 0 Δ = (−2b)² − 4*2*( b² − 4 b) = 4 b² − 8 b² + 32 b = − 4 b² + 32 b = 0 − 4 b *( b − 8) = 0 b = 0 lub b = 8 zatem y = − x + 8 =========