pomocy niedzielan: Z dwóch miast , A i B odległych od siebie o 90km wyjechali rowerami dwaj znajomi , by spotkać się o umówionej godzinie w miejscowości C znajdującej się między A i B . Pierwszy z kolegów (z miasta A) wyjechał o godzinę później niż drugi . W jakiej odległości od A znajduje się C jeśli wiemy że gdyby znajomi kontynuowali podróż po spotkaniu w C , każdy w wybranym wcześniej kierunku i z dotychczasową szybkością to pierwszy dotarłby do B w półtorej godziny zaś drugi do A w cztery godziny ?

niedzielan: błagam pomóżcie

Eta:

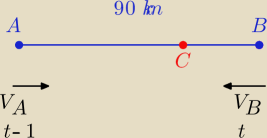
	vA		4
Na drodze AC: vA*(t−1) = vB*4 ⇒		=
	vB		t−1

	vA		t
Na drodze BC : vA*1,5= vB*t ⇒		=
	vB		1,5

	4		t
to		=		⇒ t2−t−6=0 ⇒ (t−3)(t+2)=0 ⇒ t=3h , bo t>1
	t−1		1,5

	vA
to:		= 2 ⇒ vA= 2vB ( ten co dłużej "spał" miał prędkość 2 razy większą
	vB

	90		90
na całej trasie :		= vA ⇒ vA=
	t−1+1,5		3,5

	90		180		3
to na trasie AC: |AC|= vA*(t−1) =		*2=		= 51		km
	3,5		3,5		7

	3
Odp: Miejsce spotkania wC znajduje się 51		km od miasta A
	7

pigor: ..., lub tak : niech t, t−1 − czas jazdy do chwili spotkania znajomych z B, A odpowiednio, zaś x=? szukana odległość C od A , to z warunków zadania mam np. układ równań :

t−1		4−t		x
	=		=		⇒ t(t−1)=(4−t)(1,5−t) i xt=(90−x)(4−t) ⇔
1,5−t		t		90−x

⇔ t²−t=6−5,5t+t² i xt=360−90t−4x+xt ⇔ 4,5t=6 /:1,5 i 4x=360−90t ⇔ ⇔ 3t=4 i 4x=360− 30*4 ⇒ 4x=240 ⇔ x= 60 [km] = |CA| . ...

Eta: Hej pigor ( gdzie mam błąd? ... bo tak myślałam,że coś skopałam

pigor: ..., powiem szczerze nie ma pojęcia, bo u Ciebie nic nie "grzebałem'" no i nie chce mi się ....., przepraszam; pozdrawiam.

daras: toć to samo było tydzień temu nic tylko kopiować i wklejać

Eta: daras podaj link

Eta: pigor miły jesteś i szczery do bólu

daras: Eta nie chce mi sie szukac , bo nie jestem zainteresowany , podobnie jak niedzielan, który już dawno śpi a swoją drogą, to dziwię sie,ze te posty są tu wrzucane bez ładu i składu i ca jakiś czas sie powtarzają=robota głupiego

niedzielan: jestem nie spie

daras: mi wystarczy, że raz to już rozwiązałem i pigor z raz co najmniej tez przy drugim podejściu mam juz odruch wymiotny a przy trzecim ...lepiej nie mówić

daras: skoro nie śpisz niedzielan, to kliknij w tutejsza wyszukiwarkę i Karampuk Ci sam wyskoczy z kapelusza kolorowych snów !

pigor: ..., przepraszam Eta , kurcze, że też musiałem chlapnąć tak ; a co do tego zadania, to nie rozwiązywałem go wcześniej, teraz zwróciłem na nie uwagę, ze względu na bardzo staranną jego treść, co mi się spodobało; a moje rozwiązanie − układ równań, to z wykresu z układem osi tOs . ..

Domel: pigor wg twoich obliczeń odległość |AC| czyli x = 60 km. Więc rowerzysta B pokonując tę trasę w 4 godziny jechał z szybkością 15 km/h. W takim razie początek trasy |BC| = 30 km pokonał w 2 godziny. A więc wystartował i sobie pedałuje a po godzinie po pobudce i śniadanku wystartował gość z miasta A. Ma teraz tylko godzinę, żeby dotrzeć do C czyli pędzi 60 km / h −Uffffffff (to chyba Szurkowski ). Ale w takim razie czemu się tak wlókł te ostatnie 30 km z C do B (aż 1,5 godziny) Przecież powinien to przelecieć w 0,5 godziny. Konkludując (jak ja lubię to słowo ) ja jestem za Etą

daras: dobrze zrobiłaś Eta

zawodus: Też tak twierdzę

walt: Wynik Ety jest zgodny z wynikami z różnych stron jeśli chodzi o dokładnie to zadanie.. Teraz pytanie, co zrobił źle Pigor? Rachunek jest poprawny.

pigor: ..., ale jaja kurcze, będę miał więcej czasu to pochylę się jeszcze raz nad moimi równaniam ; czyżbym źle zrozumiał treść zadania

pigor: ... tak, wszyscy macie rację, to moje równania są błedne ; choć rachunki poprawne; przepraszam ,spieprzyłem podobieństwo ΔΔ ma moim rysunku na płaszczyźnie z układem tOs, bo powinny być np. takie :

t−1		4		x
	=		=		i t >1 ⇔ t2−t=6 tx=360−4x ⇔
1,5		t		90−x

⇔ t²−7−6=0 i t>1 i x(t+4)=360 ⇔ t=3 i 7x=360 ⇔ x=51,429 km ±1m −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− P.S. a więc równania analogiczne jak Ety, którą jeszcze raz przepraszam, bo jednak trzeba było w nich ... choć co nieco, ale "pogrzebać"

Eta:

pigor: ... i ja cieszę się, że Ty się cieszysz, bo dla mnie to oznacza wybaczenie, mojego braku .. pokory; pozdrawiam.

Eta: Również ciepło pozdrawiam

daras: wielkie jest przyznać się do błedu pigor