Planimetria, pomocy! Pollyanna: W trapezie KLMN podstawami są boki KL i MN ( KL > MN ), a ponadto: KL = 20, KM =18, LN = 24. Proste KN i ML przecinają się w takim punkcie P,że PM = ML. a) Oblicz pole danego trapezu. b) Sprawdź, czy w ten trapez można wpisać okrąg.

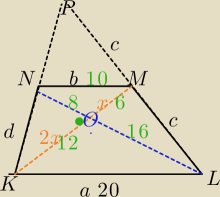
Mila: a=20 KM=18 LN=24 KL||MN ΔNMP∼ΔKLP⇔

b		a		b		a
	=		⇔		=		⇔
MP		LP		c		2c

	a		20
b=		=		=10
	2		2

	b		1
ΔNMO∼ΔKLO w skali k=		=		⇔
	a		2

OM=x i KO=2x i x+2x=18 |OM|=x=6 i KO=2*6=12 Analogicznie ON=1y , OL=2*y oraz y+2y=24 |ON|=y=8 i |OL=16| wΔNMO: b=10, OM=6, ON=8 z tw. odwrotnego do tw. Pitagorasa ⇒ 10²=6²+8² ten Δ jest prostokątny. Pozostałe Δ też. Teraz oblicz pola Δ i zsumuj.

Mila: ?)