Trapez Michał: Na okręgu opisano trapez, w którym krótsza podstawa ma długość a, a dłuższa podstawa tworzy z ramionami kąty i mierze alfa. Oblicz pole tego trapezu.

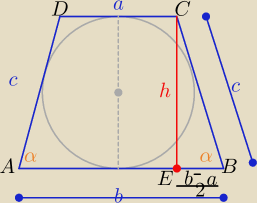
Eta: Trapez jest równoramienny ( z informacji o kątach ostrych)

	a+b
z warunku wpisania okręgu w trapez : a+b=2c ⇒ c=
	2

W trójkącie EBC

	|EB|		b−a		1+cosα
cosα=		⇒ cosα=		⇒b= a*
	|BC|		a+b		1−cosα

h		a+b
	= sinα ⇒ h= c*sinα =		*sinα
c		2

	a+b
P(tr)=[		]2*sinα=...... podstawić dane i..........
	2

	a2*sinα
P(tr)=		[j2]
	(1−cosα)2

5-latek: To jest zadanie z tego arkusza z info. (przed chwila wlasnie ogladalem) Tam musza zaplacic zeby zobaczyc rozwiazanie a tu darmowe

Eta: I dlatego "co darmowe" ....to często bez słowa dziękuję

5-latek: Nie chcialem tego nawet pisac

Eta:

Barry:

	4a2*sinα
czy pole nie powinno wyjść P =
	(1−cosα)2