Dla jakich wartości parametru p (x-3)[x^2-2(2p+1)x+(p+2)^2] równanie ma dwa różn kott: Dla jakich wartości parametru p równanie (x−3)[x²−2(2p+1)x+(p+2)²] ma dwa różne rozwiązania

J: Nie ma równania, ale zakładam ,że = 0 Skoro masz już jeden pierwiastek x = 3, to trójmian musi mieć jeden pierwiastek,Δ = 0

Godzio: Δ = 0 i x ≠ 3 lub Δ > 0 i x₁ = 3

Kaja: jednym z rozwiązań jest x=3. zatem trójmian w nawiasie kwadratowym musi mieć jedno rozwiązanie

	b
różne od 3. czyli Δ=0 i −		≠3
	2a

J: Racja "Godzio"

Godzio:

kott: Dziękuję serdecznie za pomoc. Mam tylko jeszcze jedno pytanie. Bo wartość parametru p wyszła mi inna niż w odpowiedzi. Mi wyszło tak: Δ=12{p}²−12 Więc z zał. Δ=0 i x≠3 p=1 i p0≠1 p∊zbioru pustego z zał. Δ>0 i x1=3 p>1 i p=1 lub p=7 p=7 Czyli p=7 Według odpowiedzi wynik powinien wyjść p∊{−1,7} Gdzie zrobiłam błąd?

kott: A dobrze już widzę mój błąd .

xd: To sie moze podziel z nami?

lubiewpusi: dalej czekam

123: Chcę się tylko upewnić, czy jeśli do przypadku 1° dam warunek x₀ ≠ 3, zamiast −b/2a ≠ 3 tylko f(3) ≠ 0 to czy też to jest zawsze poprawne? Gdyż dla 1 zapisu wyjdzie p ≠ 1 natomiast w drugim p ≠ 1 ale też p ≠ 7, tak samo innych zadaniach tego typu, czasami wychodzi dla zapisu −b/2a ≠ od np 1, parametr różny od na przykład 2 a dla f(1) ≠ 0 wychodzi m € R, co prawda nie wpływa to na przedział parametru z danego przypadku po wzięciu koniunkcji z deltą = 0, lecz chciałbym się upewnić że jest to równoważny zapis. Co gdyby wyszło np z warunku ∆ = 0, p = 10 a np dla −b/2a ≠ 3 wyszłoby p ≠ 10 natomiast dla f(3) ≠ 0 wyszłoby p ≠ 2 więc dla 1 zapisu byłby zbiór pusty, dla którego warunki zadania są spełnione natomiast dla 2 zapisu wyszłoby p = 10? Chyba że tak się nie może zdarzyć

I'm back: f(3) ≠ 0 nie jest wystarczające (chyba że dokładamy Δ = 0, ale wtedy p≠7 nam nie wyskoczy) Twoje dalsze dywagacje są pozbawione sensu i nie mają przełożenia na stan faktyczny. "co gdyby wyszło..." <−−− tak zwyczajnie wyjść nie może. f(3) ≠ 0 daje nam parametry p dla którego jedno z miejsc zerowych (niekoniecznie jedyne) jest równe x=3, skoro przy założeniu że ma to być jedyne miejsce zerowe wyszło nam dla p=10 (i te wartość odrzucamy) to dla warunku bardziej ogólnego czyli f(3) ≠ 0 także nam wyjdzie ta sama wartość parametru i możliwe że jeszcze inne (które mają miejsce gdy mamy dwa miejsca zerowe, w tym jedno z nich jest równe x=3)

123: No dobra, ale w jednym zadaniu wychodzi dla warunku f(0) ≠ 3 np m ≠ 2 natomiast dla x₀ ≠ 3 wychodzi m € R, więc nie wychodzi ta sama wartość − jakby przedział dla warunku f(0) ≠ 3 jest węższy

123: Albo w jeszcze innym zadaniu wychodzi dla x₀ ≠ od na przykład 2, m ≠ 1 natomiast dla f(0) ≠ 3, m ≠ 7 i obliczenia są na 100% poprawne , więc też uważam jak ty ale dlaczego dla niektórych przypadków jest jednak inaczej?

123: "f(3) ≠ 0 nie jest wystarczające (chyba że dokładamy Δ = 0, ale wtedy p≠7 nam nie wyskoczy)" Przecież dokładnie o tym pisałem wczoraj i miałem na myśli że potrzebna jest ∆ = 0, No i właśnie tak jak w tym zadaniu z tego postu, skoro. ∆ = 0 dla p = 1 a z drugiego warunki wychodzi p ≠ 1 lub p ≠ 7 to akurat i tak wyjdzie zbiór pusty

123: Odnośnie mojego postu o 5:19 to po prostu jestem śpiący i faktycznie dobrze jest, bo wychodzi ta dodatkowa wartość parametru jakby dla x₀ ≠ 3 mamy m € R + dla f(0) ≠ 3 jakaś jeszcze jedna wartość parametru, lecz zastanawia mnie jeszcze odpowiedź na post o 5:22

I'm back: Zacznijmy od tego że jaki niby jest związek pomiędzy x₀ ≠ 3 z f(0) ≠ 3 Odpowiedź brzmi ŻADEN Jakby było sprawdzane x₀ ≠ 3 oraz f(3) ≠ 0 to jeszcze bym to zrozumiał.

123: Oczywiście w każdym chodziło mi o f(3) ≠ 0!

I'm back: A o co w ogóle Ci chodzi w wypowiedź z 5.22? Co ma jedno do drugiego? Może zamiast teoretyzować pokaż przykład, pokaz obliczenia i przede wszystkim pokaż co liczysz, po co liczysz i co chcesz uzyskać.

I'm back: No to wypowiedzi 5:22 po co masz x₀ ≠ 2 i porównujesz do f(3)≠0? Co ma pies do ptaka?

123: Missclik − więc prosiłbym o odpowiedź na tamten post + jeszcze mam pytanie, zatem dobrze myślę, że nie może się zdarzyć tak, że np ( zmyślam ) dla ∆ = 0 wyszłoby m = 6, dla x₀ ≠ 3 wyszłoby m ≠ 2 ( więc mamy rozwiązanie przypadku dla m = 6 ) natomiast dla f(3) ≠ 0 wyszłoby m ≠ 2 oraz ta jeszcze jedna wartość m ≠ 6 która odrzucałaby tą wartość parametru z warunku z delty ∆ = 0 gdybyśmy zapisali w ten sposób ten warunek? I stąd wniosek że można to zamiennie "zawsze" stosować

123: "No to wypowiedzi 5:22 po co masz x0 ≠ 2 i porównujesz do f(3)≠0? Co ma pies do ptaka?" Też się pomyliłem, chodziło mi o x₀ ≠ 2 i f(2) ≠ 0 i stąd wychodzą dwie różne wartości parametru, dla pierwszego zapisu x₀ ≠ 2 wychodzi np m ≠ 1 natomiast dla f(2) ≠ 0 inna wartość parametru niż ≠ 1

wredulus_pospolitus: załóżmy (hipotetycznie) że: 1) z warunku f(3) ≠ 0 wychodzi nam: m ≠ 2 i m ≠ 6 2) z warunku Δ = 0 wychodzi nam: m = 6 tak więc z (2) mamy, że dla m = 6 mamy Δ=0 (czyli mamy jedno miejsce zerowe funkcji), natomiast z (1) mamy, że dla m = 6 funkcja ma miejsce zerowe w x₀ = 3 związku z tym −−> z tych dwóch warunków wynika, że miejsce zerowe x₀ = 3 dla parametru m = 6 jest jedynym miejscem zerowym. Co chcesz zamiennie zastosować?

	b
f(3) ≠ 0 ∧ Δ = 0 zamiennie z −		≠ 3 ∧ Δ = 0
	2a

tak ... te zestawy warunków możesz stosować zamiennie jednak warunek:

	b
f(3) ≠ 0 nie znaczy to samo co −		≠ 3 czy tam jak pisałeś/−aś: xo ≠ 3 (co
	2a

jest konsekwencją prawego zestawu warunków)

123: " f(3) ≠ 0 nie znaczy to samo co −b/2a " to to wiem, ale w takich warunkach że równanie ma mieć albo jedno rozwiązanie różne od 3 lub dwa z czego jedno jest równe 3 można zapisać, w taki sposób że pierwszy przypadek na dwa sposoby: 1° ∆ = 0 x₀ ≠ 3 bądź f(3) ≠ 0 Oraz 2° ∆ > 0 f(3) = 0 ( tylko w taki sposób drugi warunek, bo pisząc zamiast f(3) ≠ 0 tylko x₀ ≠ 3 zawężamy warunek co jest niepoprawne i nie ma sensu logicznego ) A odnośnie mojego posta dzisiaj z rana, tak więc tak jak pisałem nie może wyjść tak, że np delta, ∆ = 0 <=> m = 5, natomiast dla warunku drugiego zapisanego jako x₀ ≠ 3 → −b/2a ≠ 3 wyszłoby m ≠3, więc warunki zadania są spełnione dla m = 5, natomiast dla warunku drugiego zapisanego jako f(3) ≠ 0 wyszłaby ta wartość co dla x₀ czyli m ≠ 3 oraz ta inna wartość na przykład m ≠ 5 co by sprowadzało przypadek jako sprzeczny / niemożliwy, prawda?

wredulus_pospolitus: "f(3) = 0 ( tylko w taki sposób drugi warunek, bo pisząc zamiast f(3) ≠ 0 tylko x₀ ≠ 3 zawężamy warunek co jest niepoprawne i nie ma sensu logicznego )" co? Nie ... w drugim przypadku (dla Δ>0) piszemy f(3) = 0 dlatego ... że łatwiej jest obliczyć wartość funkcji w x=3 niż sprawdzić jakie miejsca zerowe (pierwiastki) będą i kiedy to będzie 3

	b
ależ przecież −		≠ 3 nie jest równoznaczne z xo ≠ 3 o czym pisałem o 15:11
	2a

pierwsze wskazuje na pierwszą współrzędną wierzchołka paraboli, drugie mówi nam o tym jaka jest współrzędna miejsca zerowego funkcji. To są dwie różne rzeczy

wredulus_pospolitus: Wybacz ... ale zacznijmy od początku − JASNO i konkretnie napisz o co Ci chodzi. podaj KONKRETNY przykład i podaj JASNE i KONKRETNE pytania. Szczerze mówiąc − to już nie mam pojęcia o co Ci właściwie chodzi

123: pierwsze wskazuje na pierwszą współrzędną wierzchołka paraboli, drugie mówi nam o tym jaka jest współrzędna miejsca zerowego funkcji. −b/2a jest to również wzór na miejsce zerowe funkcji kwadratowej gdy ∆ = 0, więc teraz ty piszesz brednie i nie wiem o czym mówisz Więc x₀ = −b/2a Tak więc mam tutaj pytanie nawet z tegorocznej matury rozszerzonej z czerwca https://arkusze.pl/matura-matematyka-2021-czerwiec-poziom-rozszerzony/#google_vignette Dla x₀ ≠ 3 otrzymamy wartość parametru m ≠ 5 z równania −m+1/2 ≠ 3, natomiast z f(3) ≠ 0, mamy m ≠ 3/2 i m ≠ −2/3 ( więc nie mamy oprócz wartości odrzuconej z warunku x₀ ≠ 3 i jakiejś innej jak pisał @I'm back ) I też tutaj się zastanawiam dlaczego przyjęli przypadek ∆ = 0 i x₁ ≠ 3 skoro powinno być ∆ = 0 i x₀ ≠ 3 czyli −b/2a ≠ 3 lub inaczej zapisane f(3) ≠ 0 , tzn dlaczego akurat przyjęli że x₁ ≠ 3? ) A ogólnie jeszcze raz napiszę o co mi chodzi, czy można zamiennie stosować warunki dla przypadku ∆ = 0 x₀ ≠ 2, czyli −b/2a ≠ 2 albo zamiast tego zapisać f(2) ≠ 0 i stąd otrzymamy zawsze wartość parametru, tak jak napisał @I'm back Odnośnie warunków x₀ ≠ 2 i f(2) ≠ 2 to f(2) ≠ 0 daje nam parametry p dla którego jedno z miejsc zerowych (niekoniecznie jedyne) jest różne x=2, skoro przy założeniu że ma to być jedyne miejsce zerowe, to dla warunku bardziej ogólnego czyli f(2) ≠ 0 także nam wyjdzie ta sama wartość parametru i możliwe że jeszcze inne (które mają miejsce gdy mamy dwa miejsca zerowe, w tym jedno z nich jest równe x=2)

Mila: Chodzi Ci o zadanie 12 ?

123: Tak

123: O kojarzę Ciebie Mila, może pomoglabyś rozwiać te wątpliwości? Prosiłbym o dokładną odpowiedź, tylko najpierw przeczytaj wszystkie posty

123: W razie czego przesyłam wszystko razem a jednym poście napisane trochę innymi słowami Jeśli nigdzie nie zrobiłem literówki Załóżmy, żeby jakieś równanie miało 2 rozwiązania, to równanie też załóżmy oznaczone jako (3)* któro jest kwadratowe ma mieć albo 1. Przypadek jedno rozwiązanie dwukrotne i jest ono różne od np −3 lub 2. Przypadek dwa różne rozwiązania z czego jedno jest równe −3 a drugie jakieś inne. Jeśli zapiszemy że 1° ∆ = 0 f(−3) ≠ 0 2° ∆ > 0 f(−3) = 0 To czy np w pierwszym przypadku drugi warunek jest równoważny x₀ ≠ −3 ? Bo niby taki zapis jest równoważny i tak nam mówiła Pani na lekcji, ale rozwiązując drugi warunek jako f(−3) ≠ 0 otrzymujemy m ≠ 2, a jeśli zastąpimy to jako x₀ ≠ −3, czyli to jest równe −b/2a ≠ −3 stąd −1≠3 czyli m € R, ( sama ostateczna wartość parametru i tak wyjdzie taka sama w tym przypadku m = −3 ) dla pierwszego warunku: ∆ = 0 <=> m = −3, więc nie ma to wpływu na wartość parametru m dla której warunki zadania da spełnione ) Albo w innym zadaniu dla takich samych warunków dla zapisu f(2) ≠ 0 wyjdzie m ≠ −1, a dla x₀ ( bo w tym przypadku równanie ma jedno rozwiązanie ( delta = 0 ) ) wyjdzie np −b/2a ≠ 2 <=> m ≠ −4 , co też co prawda nie wpływa na wartość parametru m dla tego przypadku, bo np dla pierwszego warunku ( zmyślam, bo dokładnej wartości nie pamiętam ale to nie ma tutaj znaczenia i np ∆ = 0 <=> m = 10 , ale jednak nie daje mi to spokoju czy tak można to zapisywać. Bo jeśli ( nie wiem czy tak się może zdarzyć, bo *podobnie* jest w zadaniu maturalnym które opiszę poniżej i dam link ) że ∆ byłaby równa 0 <=> m = 5, a z zapisu f(3) ≠ 0 wyszłoby m ≠ 5 oraz inna wartość a dla zapisu x₀ ≠3 <=> m ≠ jakiejś innej wartości niż 5, na przykład m ≠ 7 to dla 1 zapisu wartościami m dla których warunki zadania są spełnione byłby zbiór pusty a dla drugiego zapisu m = 5 , ****do tego będzie odwołanie na sam koniec postu Żeby to lepiej pokazać, tak więc mam tutaj pytanie nawet z tegorocznej matury rozszerzonej z czerwca https://arkusze.pl/matura-matematyka-2021-czerwiec-poziom-rozszerzony/#google_vignette Dla x₀ ≠ 3 otrzymamy wartość parametru m ≠ 5 z równania −m+1/2 ≠ 3 natomiast z f(3) ≠ 0, mamy m ≠ 3/2 i m ≠ −2/3 ( więc nie mamy oprócz wartości odrzuconej z warunku x₀ ≠ 3 i jakiejś innej dodatkowej ze względu na dwa miejsca zerowe co napiszę poniżej ****) I też tutaj się zastanawiam dlaczego przyjęli przypadek ∆ = 0 i x₁ ≠ 3 skoro powinno być ∆ = 0 x₀ ≠ 3 czyli −b/2a ≠ 3 lub inaczej zapisane jako f(3) ≠ 0 tzn dlaczego akurat przyjęli drugi warunek jako x₁ ≠ 3 ? ) **** ogólnie jeszcze raz napiszę o co mi chodzi, czy można zamiennie stosować warunki dla przypadku ∆ = 0 x₀ ≠ 2 czyli −b/2a ≠ 2 albo zamiast tego zapisać f(2) ≠ 0 i stąd otrzymamy zawsze wartość parametru, tak jak w zdaniu poniżej f(2) ≠ 0 ^daje nam wartości parametru dla których jedno z miejsc zerowych (niekoniecznie jedyne) jest różne od "2", skoro przy założeniu że ma to być jedyne miejsce zerowe, to dla warunku bardziej ogólnego czyli f(2) ≠ 0 także nam wyjdzie ta sama wartość parametru i możliwe że jeszcze inna (które mają miejsce gdy mamy dwa miejsca zerowe, w tym jedno z nich jest równe, x = 2

I'm back: @123 − na całość odpisze wieczorem, ale już widzę błąd logiczny f(3) ≠ 0 znaczy dokładnie to samo co zapis x₀ ≠ 3 Ale zapis x₀ ≠ 3 nie znaczy tego samego co zapis − b/2a ≠ 3

Mila: 1) Zadanie: Dla jakich wartości parametru p równanie: (*) (x−3)[x²−2(2p+1)x+(p+2)²] =0 ma dwa różne rozwiązania x−3=0 lub x²−2(2p+1)x+(p+2)²=0 2) Dla jakich wartości parametru m równanie : (x−3)*(x²+(m−1)x−(m²+2m) )=0 ma dokładnie dwa rozwiązania.

	2		1		3
W tym zadaniu jest odp. m∊{−		,		,		}
	3		5		2

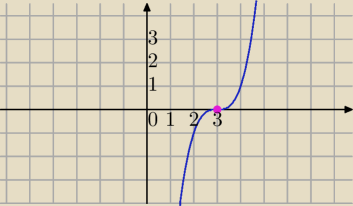
============================================ Ad 1) x=3 jeden z pierwiastków a) Sprawdzamy jaką wartość ma p gdy x=3 jest rozwiązaniem równania x²−2(2p+1)x+(p+2)²=0 9−2(2p+1)*3+(p+2)²=0 p=1 lub p=7 b) sprawdzamy jaki jest drugi pierwiastek p=1 x²−2*3x+9=0 x²−6x+9=0 (x−3)²=0 czyli x₁= x₂=x₃=3 równanie (*) ma jedno rozwiązanie ( ilustracja niebieska) zatem p≠1 c) p=7 x²−2(14+1)x+81=0 x²−30x+81=0 x=3 lub x=27 Pasuje. dla p=7 mamy dwa rozwiązania. x₁=x₂=3 oraz x₃=27 2.2 Δ=4(2p+1)²−4(p+2)² Δ=12p²−12 12(p²−1)=0 p=1 lub p=−1 p=1 nie odpowiada nam (patrz pkt (b)) sprawdzamy p=−1 x²+2x+1=0 (x+1)²=0 x=−1 dołączając x=3 mamy dwa rozwiązania dla x<−1 lub x>1 may dwa różne rozwiązania co daje 3 rozw, równania (*) ========== odp. p∊{−1,7} Teraz analizuj rozwiązanie zadania (2)

Pr713 : No dobrze, ale to dobrze zrozumiałem, że jest to równoważne? f(3) ≠ 0 znaczy dokładnie to samo co zapis x₀ ≠ 3 I zapis x₀ ≠ 3 znaczy to samo co zapis − b/2a ≠ 3 *w przypadku 1° gdy ∆ = 0 i można to wtedy stosować zamiennie tzn f(3) ≠ 0 i x₀ ≠ 3?