nd dowodzenie zela: Przez środek D przyprostokątnej BC trójkąta prostokątnego ABC poprowadzono prostą prostopadłą do przeciwprostokątnej AB. Prosta ta przecina proste AB i AC odpowiednio w punktach M i N.

	2cosα
Wykaż, że skala podobieństwa trójkątów ABC i ANM jest równa
	1+cos2α

z góry dzieki

zela: prosze o pomoc bo siedze nad tym i nadal nie wiem jak to zrobić

Eta:

	2x
Trójkąty podobne ANM i ABC z cechy (kkk) o skali podobieństwa k=
	|MN|

	|MD|
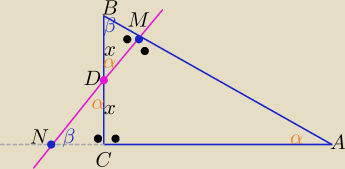
W ΔMBD :		= cosα ⇒ |MD|=x*cosα
	x

	x		x
i w ΔNCD :		=cosα ⇒ |DN|=
	|DN|		cosα

|MN|= |MD|+|DN|

	2x
to: k=		= ..... dokończ
	x   x*cosα+   cosα

zela: dzieki

Eta:

pigor: ...,to jeszcze do mojej. "szuflady" : niech |DM|=b, |DN|=c dla uproszczenia zapisu, to

	|AC|		2x		2*xc		2*xc
k=		=		=		=		=
	|MN|		c+b		1+bc		1+bx*xc

	2cosα		2cosα
=		=		c.n.w. . ...
	1+cosα*cosα		1+cos2α