ciagi
gosiata: | | 3 | |
wykaż że ciąg an= 1 + |
| jest malejący |
| | n | |
9 mar 11:55
gosiata: mam korzystać ze wzoru: an+1 − an ?
9 mar 11:58
52: Kiedy ciąg jest malejący ?
9 mar 12:01
Tadeusz:
... z takiego jakiego Ci wygodniej
A możesz też zauważyć, że kolejne wyrazy ciągu układają się na wykresie
9 mar 12:02
Tadeusz:
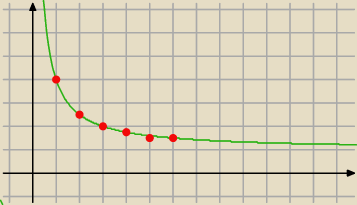
9 mar 12:03
gosiata: 52 , kiedy an<0
Dziekuje Tadeusz
a nie ma innego sposobu wlasnie cos ze wzorami?
9 mar 12:10
gosiata: znaczy an+1−an < 0
9 mar 12:11
Tadeusz:
przecież napisałem, że możesz różnie ... jak Ci wygodniej
rosnący gdy:
a
n+1−a
n>0
lub
9 mar 12:13
gosiata: ok ok , dziękuje
| | 3 | | 3 | | 3 | |
an+1 − an = 1 + |
| − 1 − |
| = − |
| czyli ciag malejący, db? |
| | n+1 | | n | | n(n+1) | |
9 mar 12:17
gosiata: ok ok , dziękuje
| | 3 | | 3 | | 3 | |
an+1 − an = 1 + |
| − 1 − |
| = − |
| czyli ciag malejący, db? |
| | n+1 | | n | | n(n+1) | |
9 mar 12:17
fx: | | 3 | |
Czyli po prostu gdy dla przyrostu n obserwujemy spadek wartości ciągu. Ciąg 1 + |
| − widać |
| | n | |
| | 3 | |
od razu, że dla przyrostu n, wyrażenie |
| jest malejące, stąd wniosek, że ciąg jest |
| | n | |
malejący.
9 mar 12:17
omi:
| | 3 | | 3 | | 3n−3(n+1 | | −3 | |
an+1−an= 1+ |
| − 1− |
| = |
| = |
| <0 |
| | n+1 | | n | | n(n+1) | | n(n+1) | |
bo n(n+1)>0 dla n∊N+
to ciąg a
n jest malejący
9 mar 12:17