proszę o pomoc w rozwiązaniu tych zadań, trochę ciągów, trochę innych rzeczy Agata: bardzo proszę o pomoc w rozwiązaniu tych zadań 1. W trapezie równoramiennym krótsza podstawa ma długość 3 cm, przekątna ma 12 cm, a wysokość jest równa 6 cm. Oblicz pole tego trapezu. 2. α, β, γ oznaczają kąty trójkąta, zaś a, b, c długości przeciwległych boków. Rozwiąż ten trójkąt, wiedząc, że a= 4√3, b=4, α=60 stopni.

	n+3
3. Zbadaj monotoniczność ciągu an=
	2n

	1		1
4.W pewnym ciągu arytmetycznym a1= 3		i r=
	2		3

	1
a) Którym wyrazem ciągu jest liczba 14		?
	6

b) Sprawdź, czy liczba 102 jest wyrazem tego ciągu.

	5n
5. Dany jest ciąg geometryczny określony wzorem ogólnym an=		. Wyraz drugi i czwarty
	3

tego ciągu są odpowiednio trzecim i jedenastym wyrazem pewnego ciągu arytmetycznego (bn). Suma ilu początkowych wyrazów tego ciągu (bn) est równa 1150? 6. Dany jest trójkąt prostokątny o bokach długości 3 cm, 4 cm i 5 cm. Oblicz długości odcinków, na które dwusieczna kąta prostego dzieli przeciwprostokątną. 7. Pole trapezu wynosi 224 cm², zaś wysokość trapezu jest o 2 cm większa od długości odcinka łączącego środki boków nierównoległych trapezu. Oblicz długość podstaw tego trapezu, wiedząc że och różnica wynosi 6 cm.

5-latek: Zadanie nr 6 zastosuj twierdzenie o dwusiecznej kata wewnetrznego

5-latek: Zadanie nr 3 zbadaj roznice a_n+1−a_n

Godzio: 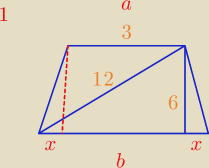Zad. 1

	b − a
x =
	2

Z twierdzenia PItagorasa: (b − x)² + 6² = 12² ⇒ (b − x)² + 36 = 144 ⇒ (b − x)² = 108 ⇒ b − x = 6√3

	b − a
b −		= 6√3 ⇒ 2b − (b − 3) = 12√3 ⇒ b + 3 = 12√3 ⇒ b = 12√3 − 3
	2

	a + b		3 + 12√3 − 3
P =		* h =		* 6 = 36√3
	2		2

Zad. 2 Z twierdzenia sinusów:

a		b		c
	=		=
sinα		sinβ		sinγ

4√3		4		√3		1		1
	=		⇒		=		⇒ sinβ =
sin60o		sinβ		√3   2		sinβ		2

β = 30^o ⇒ γ = 90^o ⇒ jest to trójkąt prostokątny więc: a² + b² = c² ⇒ 48 + 16 = c² ⇒ c = 8 Zad. 3

	7		1		1		21		1		2
an = a1 + (n − 1) * r =		+		n −		=		+		n −
	2		3		3		6		3		6

	1		19		1		85
an =		n +		= 14		=
	3		6		6		6

1		66
	n =		= 11
3		6

n = 33 Jest to 33 wyraz a_n = 102 / * 6 ⇒ 2n + 19 = 612 ⇒ 2n = 593 −− liczba nieparzysta, więc n nie jest liczbą naturalną, stąd nie jest to wyraz ciągu

Godzio: Zad. 3 to Zad. 4

5-latek: Tylko to miala byc pomoc a nie gotowce .

Agata: Jestem na studiach gdzie nie uczę się już matematyki i mi to do niczego nie jest potrzebne. Te zadania są dla mojego brata który dokształca się w technikum uzupełniającym, zależy mu na nowym zawodzie nie na maturze , którą już ma także gotowce mile widziane

X: Demoralizacja.

Mila: I dlatego 5−latku pomagajmy kapryśnemu nieco Radkowi, bo on chce się nauczyc. Będzie w przyszłości uczciwym obywatelem.

Agata:

	c		d
W zadaniu 6 po zastosowaniu tego twierdzenia wychodzi		=		i co dalej z tym?
	3		4