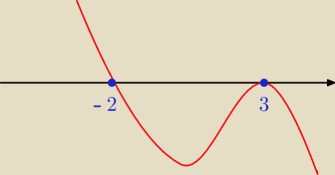
Pewne zadanko FHA: Funckaj wielomianowa y = W(x) ma dwa rózne miejsca zerowe x₁ = −2 x₂ = 3 sw. W(x) = 3 x₂ −> pierwiastek 2 − krotny W(1) = −12 a) Napisz wzór w postaci ogolnej no to mam: −x³ + 4x² + 3x − 18 b) Rozwiaz rownanie W(x) = 2x² − 12 x + 18 więc: −x³ + 4x² + 3x − 18 = 2x² − 12 x + 18 I nie chce mi wyjśc Pewnie robie glupo bląd, pozna pora c) czyli: −x³ + 4x² + 3x − 18 ≥ 0 tak?

wredulus_pospolitus: co onzacza: "sw. W(x) = 3"

Trivial: a) W(x) = −(x+2)(x−3)² = ... b) 2x² − 12x + 18 = 2(x² − 6x + 9) = 2(x−3)² Czyli: −(x+2)(x−3)² = 2(x−3)² (x−3)²(x+4) = 0 ... c) nie ma polecenia.

wredulus_pospolitus: b) gdybyś zostawił w postaci iloczynowej to: W(x) = (x+2)(x−3)² i masz: (x+2)(x−3)² = 2x² − 12x + 18 (x+2)(x−3)² = 2(x²−6x+9) (x+2)(x−3)² = 2(x−3)² stąd: (x+2) = 2 ⋁ (x−3)² = 0

FHA: c) zbior argumentow dla ktorych funkcja W przyjmuje wartosci nieujemne

FHA: up

FHA: c) zbior argumentow dla ktorych funkcja W przyjmuje wartosci nieujemne

52: Tak.

Trivial: Po co to wymnażasz w ogóle. Wymnożony wynik potrzebny jest tylko w punkcie a). c) −(x+2)(x−3)² ≥ 0 ⇒ x∊(−∞,−2]∪{3}.