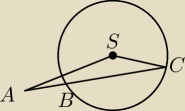
geometria Lala: dane |AS|=16, |AC|=20 oblicz |BC|, promień okręgu wynosi 8. nie mam pomysłu na to zadanie, myślałam by odległość |BC| oznaczyć sobie jako 20−x a |AB|=x i jakoś z twierdzenia cosinusów liczyc ale kąt BSC nie jest ładny , jego cosinusa nie da się odczytać z tablic bo kąt nie ma pełnej wartości. mógłby mi ktoś podsunąć jakiś pomysł..

Lala: prosze o pomoc

pigor: ..., niech |BC|=x=? , to z tw. o 2−óch siecznych z punktu nie leżącym na okręgu, masz równanie np. |AC|* |AB|= (|AS|+r)* (|AS|−r) ⇔ 20(20−x)= (16+8)(16−8) ⇔ ⇔ 20(20−x)= 24*8 /:2 ⇔ 10(20−x)= 96 ⇔ 20−x= 9,6 ⇔ ⇔ x= |BC|=10,4 − szukana długość odcinka BC . ...