własności funkcji albin55: proszę o sugestię w rozwiązaniu zadania / bez użycia pochodnych/ Wykaz ze f(x)=x³−x²+x jest rosnąca w R

Olcia: f(x)=x(x²−x+1) x(x²−x+1)>0

albin55: dziękuję −mam to − z tym , że przyrównywanie do zera chyba jest nie potrzebne. Funkcja jest ciagła ma jedno m−ce zerowe a wyrażenie w nawiasie jest zawsze dodatnie .

J: Nikt tu nic nie udowodnił, jak do tej pory

Olcia: x(x²−x+1)>0 x=0 i x²−x+1=0 delta=b²−4ac delta=1−4 delta=−3 (brak miejsc zerowych) Więc jedynym miejscem zerowym jest −3 i teraz rysujesz wykres tam gdzie to kułko to jest −3. I widzimy że x są ujemne dla (−niesk;−3> i dodatnie (3; niesk) wynik (3; niesk)

Bizon: tylko skąd te −3 −

J: Wykazałaś jedynie,że dla x > 0 funkcja przyjmuje wartości dodatnie, a w treści zadania jest powiedziane: " wykaż,że funkcja jest rosnąca w R.

Olcia: aaa sr. delta=0. i tam gdzie kółko jest 0. A więc wynik (0 do niesk). Zbiór liczb rzeczywistych to wszystkie liczby wymierne, całkowite dodatnie, ujemne czyli dokładniej wszystkie liczby. A więc nie musimy tego stawiać jako założenia. A więc po prostu dla jakich x funkcja przyjmuje wartości dodatnie.

Olcia: Jednynym miejscem zerowym jest 0.

J: Co ma miejsce zerowe do monotoniczności funkcjji ?

Aerodynamiczny: Ta funkcja może wywijać niekoniecznie w obrębie osi OX

ICSP:

	1		2		1
f(x) = x3 − x2 + x = (x −		)3 +		x +
	3		3		27

zatem f(x) jest rosnąca jako suma dwóch funkcji rosnących

Olcia: Aj przepraszam, źle mam.

Trivial: No w końcu. ICSP pokazał.

ICSP:

albin55: ....dowód ICSP jest mocny − ale czy funkcja ciągła w R posiadająca jedno miejsce zerowe nie jest ścisłe monotoniczną ? − zatem skoro wyrażenie w nawiasie jest zawsze dodatnie wiec jest ona rosnaca. Tak myślę − czy się mylę

albin55: aha bardzo dziekuje za zainteresowanie i pomoc

zawodus: mylisz się weźmy funkcję x²+2x+1 − jedno miejsce zerowe, a funkcja nie jest monotoniczna w dziedzinie.

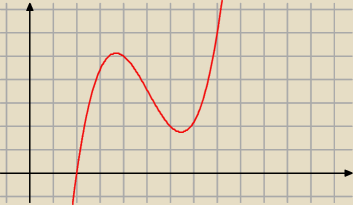
Trivial: Nie jest.

albin55: faktycznie myle sie −moze wywijać i to mocno