jerey: jak znaleźć długosc y? ac = cb =1 kombinowałem z podobienstwem trojkatów adc i abd

√2		1
	=
1		1−x

po wyznaczeniu x'a z pitagorasa y?

jerey:

√2		x
	=		* ⇒x=2−√2
1		x−1

Tadeusz: zapisz porządnie treść |AB|=√2 ... to też dane ?

pigor: ..., jak rozumiem te wielkie kropy czarne, to kąt prosty, no to np. tak :niech jeśli |bd|= x ⇒ |cd|=1−x , a wtedy ?=y² = 1²−(1−x)² = (√2)²−x² ⇒ 1−(1−x)² = 2−x² i licz x .

Antek: Jesli jest tak jak napisales ze cb=1 to zauwaz ze y bedzie wysokoscia tego trojkata bo pada na bok cb pod katem prostym .

	1
Wiec 2 wzory na pole np wzor herona i drugi P=		a*h
	2

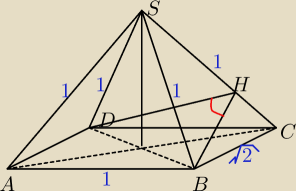
jerey: tak. oto zadanie. Podstawą ostrosłupa ABCDS jest prostokąt ABCD , w którym AB = 1 , BC = √2 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.

	√3
w trójkat DCS jest równoboczny zatem DH = h ⇒
	2

AB mozemy wyliczyc z pitagorasa DB= √3 i teraz jest kłopot z BH, probowałem to wyliczyc tak jak wyzej układając proporcje z trójkątów podobnych.

jerey: ok, dzieki wam

Tadeusz: ... nie chce się gostkowi napisać porządnie zadania ... i zgaduj zgadulę urządzacie. Czy trójkąt równoramienny w którym znamy tylko długość ramion jest określony? Co chcecie policzyć?

Tadeusz: ... a jeśli dany jet również |BC|=√2 ... to jaki to trójkąt (równoramienny o bokach 1 i 1 oraz podstawie √2)

jerey: prostokątny ................

jerey: tzn. połowa kwadratu

Tadeusz: ... i wszystko jasne −