Planimetria bezendu: Suma długości dwóch boków trójkąta jest równa 12cm, a kąt między tymi bokami ma miarę 120^∘ . Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe c²=a²+b²−2abcosα

	1
c2=(12−b)2+b2−[2(12−b)b*−		)]
	2

c²=144−24b+2b²−[(24b−2b²)*(−0,5)] c²=144−24b²+2b²+12b−b² c²=b²+12b+144 I coś się nie zgadza

Maslanek: A nie lepiej skorzystać z miejsca ze wzoru na pole? Panie drogi

zawodus: co się nie zgadza? Jak się liczy pole trójkąta?

bezendu: Ja muszę szukać wartości największej a tutaj parabola ramionami do góry więc znajdę wartość najmniejszą...

Maslanek: Ale liczysz długość trzeciego boku Przeczytaj polecenie

Saizou : podpowie sinus

zawodus: Nie podpowiadać! Niech chłopak sam przeczyta polecenie jeszcze raz

Saizou : ale to sinus podpowiada xd

bezendu: Ale to jest zadanie na ekstrema więc musi być f.kwadratowa. ?

Saizou : Zinterpretuj Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe

Mila: Podpowiedź, zmień kolejność, najpierw najmniejsze pole z tego co masz.

	1
PΔ=		a*b*sin(120o) i a+b=12
	2

Gdy obliczysz a i b, to tw. cosinusów

bezendu: Długości boków muszą być jak największe ?

Saizou : Mila, bezendu miał sam do tego dojść, a sinus podpowiadał

bezendu: Ale czemu mój zapis jest niepoprawny ?

Mila: A gdzie tam masz pole? Masz błąd w rachunkach c²=b²−12b+144

bezendu: Ale wyznaczę bok b z funkcji kwadratowej to policzę również bok c ?

Maslanek: Hmm... Ze względu na to, że bok "b" jest zależny od tego jakie przyjmiemy "a", więc wartość "c" też jest płynna. Trzeba zrozumieć, że wyznaczenie największego "c" nie oznacza, że dostaniemy największe pole. Bo dla tego "b" wielkość "a" może się okazać stosunkowo mała .

zawodus: Trzeba po prostu zrozumieć do końca treść zadania i nie szukać "na siłę" funkcji kwadratowej

muflon: P=absin(kąta między ab)/2 a+b=12 b=12−a a(12−a)sin(120)/2 sin 120/2 const a(12−a), masz parabole z maximum

bezendu: mulfon skopiowałeś to co napisała Mila a ja pytałem o coś innego.

pigor: ..., no to patrz i ... , bo pokombinuję co nieco np. tak : −−−−−−−−−−−−−−−−−−−−−−−−−−− a+b=12 i P_Δ= ¹₂absin120^o= ¹₂absin60^o= ¹₂ab¹₂√3= = ¹₄√3*¹₂*2ab ≤ ¹₈√3*(a+b)²= ¹₈√3*12²= = ¹₄√3*6*12= ¹₄√3*6*6*2= ¹₄(6√2)²√3 − pole Δ równobocznego o bokach długości 6√2 ma największe pole . ..

Mila: Najpierw a i b dla najmniejszego pola a potem policzysz c bo masz wzór na c 21:28.

bezendu: Ok.

bezendu: Tamto zadania wydaję się bez sensu jak dla mnie z tym polem Suma długości dwóch boków trójkąta równa się 4, a kąt między tymi bokami ma miarę 120^∘ . Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta. I tutaj też mam liczyć pole jak mogę od razu z tw cos ?

Mila: Tutaj masz zupełnie inne zadanie. Wczytaj się w tamto zadanie , tam miał być dobrany trzeci bok, gdy pole Δ ( zależne od danych boków) miało być najmniejsze. Tu nie ma mowy o warunku na pole. Zaczynasz dowolnie.

bezendu: Pole miało być największe, czyli długości boków jak najdłuższe.

bezendu: ?

Mila: O co chodzi?

bezendu: ''tam miał być dobrany trzeci bok, gdy pole Δ ( zależne od danych boków) miało być najmniejsze. '' A nie największe ?

Mila: Tak, największe , to przejęzyczenie, ale przeciez już tamto rozwiązałeś?

Mila: Dobranoc.

bezendu: Dobranoc. Jutro wracam do tych zadań.

bezendu: Pierwszego zadania nadal nie zrobiłem bo nie rozumiem.

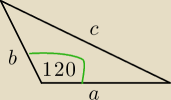
Mila: a+b=12 Kiedy pole tego Δ jest największe? No to obliczamy pole.

	1
PΔ=		*a*b*sin120o
	2

b=12−a i a∊(0,12)

	1
PΔ=		*a*(12−a)*√3{2}
	2

	√3
PΔ(a)=		*(12a−a2} wykresem jest parabola skierowana w dół. Funkcja ma wartość
	4

największą dla

	−12
aw=		=6
	−2

a=6 b=6 Teraz obliczysz c z tw. cosinusów.

bezendu: Dziękuję teraz w końcu zrozumiałem.

Mila: rozwiąż klasę II. Zadania nie są banalne.

Mila: http://www.wsip.pl/upload/2014/02/matematyka_pr_arkusze.pdf

Marcin: Macie inny link do tej matury z WSiPu? ten mi nie działa.

bezendu: Dziękuję i z okazji Dnia Kobiet

Mila: Dziękuję

Itai: BEZENDU, TAKIEGO PROSTEGO ZDANIA NIE MOGŁEŚ /AŚ ROZWIAZAĆ? MOŻE CI LINK PODAĆ CO?

bezendu: Ja już rozwiązałem i żałosny nie bądź

derekk: ma ktos zadanka z ten matury rozszerzonej z wsipu?