Planimetria
bezendu:
W zbiorze prostokątów wpisanych w okrąg o promieniu R znajdź prostokąt o największym polu.
7 mar 20:31
Tadeusz:
... na pewno kwadrat −
7 mar 20:32
bezendu:
Proszę o dalsze wskazówki
Tadeusz planimetria to nie jest moja mocna strona.
7 mar 20:33
Saizou :
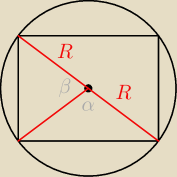
np. podpowiedź rysunek
7 mar 20:38
pigor: ... np.
P
p=
12(2R)
2sinα= ...
7 mar 20:54
Tadeusz:
... licz pole i optymalizacja −
7 mar 20:54
bezendu:
x2+y2=4R2
i dalej ?
7 mar 20:56
MQ: Jeśli zauważysz, że α+β=π, to dojdziesz do czegoś takiego jak pigor, a wtedy pole jest
maksymalne, gdy sinα=1
7 mar 21:00
pigor: ..., no właśnie, słuchaj
MQ , bo np. tak |sinx|≤ 1, więc :
P
p=
12(2R)
2sinα ≤
12*4R
2= 2R
2}=(R
√2}
2 − kwadrat o boku R
√2.
7 mar 21:19
bezendu: Dziękuję Panowie.
7 mar 21:23
+-: y=
√4R2−x2
P=x*
√4R2−x2=
√4x2R2−x4
P
max→x→P'=0→x=
√2R
7 mar 22:15
bezendu:
też wyszło mi
√2R
27 mar 21:57
Mila:
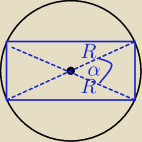
| | 1 | |
P▭=4* |
| R2sinα największa wartość dla sinα=1⇔ α=90o⇔ |
| | 2 | |
prostokąt jest kwadratem.
27 mar 23:18
bezendu:
Musiałem wrócić do tego zadania, ale odp już teraz się zgadza. Dziękuję za zainteresowanie
27 mar 23:21
Mila:
Kwadrat o przekątnej 2R.
27 mar 23:23