Znajdź pierwiastki równania kwadratowego. Matematyczka: Wyznacz wszystkie wartości parametru M, dla których równanie x² − 4mx + 3m² − 3m + 10 = 0 ma dwa różne pierwiastki rzeczywiste x1 ,x2 takie,że 1/x1 + 1/x2 < 2m

ICSP:

1		1		x1 + x2		−b
	+		=		= //ze wzorów Viete'a // =		gdzie a,b,c
x1		x2		x1 * x2		c

są współczynnikami funkcji kwadratowej zdefiniowanej : f(x) = ax² + bx + c dla a ≠ 0

J: Zacznij od tego, że musisz wyznaczyć m,dla którego trójmian ma dwa rózne pierwiastki.

Matematyczka.: Mam problem w nierówności po podstawieniu za b i c. Delta wychodzi ujemna.

Aerodynamiczny: Jak to robilem wczoraj to mi wyszlo ze m ∊ (0;2)

ICSP: Dwa warunki : 1^o Δ > 0 ⇒ m ∊ (−5 ; 2)

	−b
2o		< 2m
	a

4m
	< 2m
3m2 − 3m + 10

4m < 2m(3m² − 3m + 10) ⇒ m > 0 Ostateczne rozwiązanie to iloczyn rozwiązań z dwóch przypadków : m ∊ (0 ; 2)

Aerodynamiczny: Haha czyli dobrze zrobilem, tylko ja nie uzylem wzorow vietea i musialem sie troche naliczyc bo mialem wielomiany 3 stopnia

Mila: No, chyba jednak źle.

ICSP: ?

Mila: Przelicz Δ.

ICSP: w pkt 1^o czy w pkt 2^o ?

Mila: 1^o

ICSP: Δ = 16m² − 12m² + 12m − 40 = 4m² + 12m − 40 = m² + 3m − 10 = m² + 5m − 2m − 10 = = (m+5)(m−2) > 0 ⇒ m ∊ (− 5 ; 2)

ICSP: co prawda zgubiłem 4 w pewnym momencie, ale na rozwiązanie nierówności nie ma ona wpływu.

Mila: Odpowiedź źle.

ICSP: Faktycznie 1^o m ∊ (− ∞ ; −5) ∪ (2 ; + ∞) zatem dostajemy ostatecznie m > 2

Mila:

...: 4m < 2m(3m2 − 3m + 10) ⇒ m > 0 możesz mi to dokładniej rozpisać? Bo nadal nie rozumiem czemu m jest większe od zera?

ICSP: https://matematykaszkolna.pl/strona/142.html

natalkaa: Wstawiłby ktoś zadanka z tej matury z poziomu rozszerzonego? Chociaż kilka Będę bardzo wdzięczna

marty: Kąt rozwarty rombu ma miarę 135°, a pole tego rombu jest równe 2 36 2 cm . Bok rombu ma długość

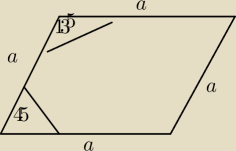
5-latek: Kat ostry rombu wynosi

360−(2*135)
	= 45
2

Wzor na pole rombu P=a²*sinalfa i wylicz a